[Paper Reivew] Classifier-Free Diffusion Guidance (CFG)

NeurIPS Workshop 2021. [Paper]
Jonathan Ho, Tim Salimans
Google Research, Brain team
28 Sep 2021

들어가며,,

Diffusion Models Beat GANs on Image Synthesis에서 제시한 Classifier Guidance(CG) 의 문제점을 지적하며, Classifier를 사용하지 않으면서(CFG) 비슷한 효과를 내는 방법론을 제시한 Google Research 논문입니다.

틀린 내용이 있다면 댓글로 알려주세요!

1. INTRODUCTION

Dhariwal & Nichol은 classifier guidance(CG) 방법론을 제시하였다. Classifier의 gradient를 활용하여 label이 있는 데이터셋에서 이미지 생성 품질을 높여 GAN보다 우수한 성능을 달성할 수 있었다.

하지만, 저자들은 CG가 다음과 같은 문제점을 가지고 있다고 지적한다.

• 별도의 classifier가 필요하므로 학습 파이프라인을 복잡하게 한다. (심지어 noisy한 이미지에 classifier가 학습되어야 하므로, pre-trained classifier를 사용할 수도 없다)
• classifier-guided diffusion sampling은 image classifier에 대한 gradient-based adversarial attack으로 생각할 수 있다는 점이다. (이는 단순히 FID나 IS score를 올리기 위한 방법정도로 간주할 수 있다)

이러한 맥락에서, 저자들은 classifier가 없는 classifier-free guidance를 제안한다. classifier를 사용하는 대신, conditional diffusion model과 unconditional diffusion model 의 score estimate를 mixing해 사용하는 방법이다.

2. BACKGROUND

저자들은 continuous time에서 diffusion model을 학습한다. \(x \sim p(x)\), \(z = \{z_\lambda \vert \lambda \in [\lambda_\textrm{min}, \lambda_\textrm{max}]\}\)라 하고, 이때 \(\lambda_{\textrm{min}} < \lambda_{\textrm{max}} \in \mathbb{R}\) 인 hyper parameter이며 forward process \(q(z \vert x)\)는 variance-preserving Markov process이다.

\[\begin{aligned} q(z_\lambda | x) &= \mathcal{N}(\alpha_\lambda x, \sigma_\lambda^2 I), \quad \quad \textrm{where} \quad \alpha_\lambda^2 = \frac{1}{1+e^{-\lambda}}, \; \sigma_\lambda^2 = 1 - \alpha_\lambda^2 \\ q(z_\lambda | z_{\lambda'}) &= \mathcal{N}\bigg(\frac{\alpha_\lambda}{\alpha_{\lambda'}} z_{\lambda'}, \sigma_{\lambda | \lambda'}^2 I \bigg), \quad \quad \textrm{where} \quad \lambda < \lambda', \; \sigma_{\lambda | \lambda'}^2 = (1 - e^{\lambda - \lambda'}) \sigma_\lambda^2 \end{aligned}\]

여기서 \(\lambda = \log (\alpha_\lambda^2 / \sigma_\lambda^2)\)이므로, \(\lambda\)를 \(z_\lambda\)의 log signal-to-noise ratio로 생각할 수 있다. Forward process는 \(\lambda\)가 작아지는 방향으로 진행된다.

---

\(x\)로 conditioning하면 forward process는 transition \(q(z_\lambda' \vert z_\lambda, x) = \mathcal{N}(\tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x), \tilde{\sigma}_{\lambda' \vert \lambda}^2 I)\) 를 반대로하여 나타낼 수 있다.

\[\begin{equation} \tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x) = e^{\lambda - \lambda'} \bigg(\frac{\alpha_\lambda'}{\alpha_{\lambda}}\bigg) z_{\lambda} + (1 - e^{\lambda - \lambda'}) \alpha_{\lambda'} x, \quad \quad \tilde{\sigma}_{\lambda' \vert \lambda}^2 = (1 - e^{\lambda - \lambda'}) \sigma_{\lambda'}^2 \end{equation}\]

---

Reverse process는 \(p_\theta (z_{\lambda_\textrm{min}}) =\mathcal{N}(0, I)\)로부터 시작한다.

\[\begin{equation} p_\theta (z_{\lambda'} | z_\lambda) = \mathcal{N} (\tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x_\theta (z_\lambda)), (\tilde{\sigma}_{\lambda' \vert \lambda}^2)^{1-v}(\sigma_{\lambda \vert \lambda'}^2)^v) \end{equation}\]

reverse process에서는 반대로 \(\lambda_\textrm{min} = \lambda_1 < \cdots < \lambda_T = \lambda_\textrm{max}\)인 방향으로 진행되며, 모델 \(x_\theta\) 가 정확하다면, \(T\)가 무한대로 갈 때, \(p(z)\)로 분포된 SDE로부터의 sample을 얻을 수 있다.

DDPM과 동일하게 \(\begin{equation} x_\theta (z_\lambda) = \frac{z_\lambda - \sigma_\lambda \epsilon_\theta (z_\lambda)}{\alpha_\lambda} \end{equation}\)로 parameterization하여 \(\begin{equation} \mathbb{E}_{\epsilon, \lambda} \bigg[ \| \epsilon_\theta (z_\lambda) - \epsilon \|_2^2 \bigg] \end{equation}\)를 objective function으로 사용한다. 이때 \(\epsilon \sim \mathcal{N} (0,I)\)이며, \(z_\lambda = \alpha_\lambda x + \sigma_\lambda \epsilon\)이다.

---

conditional 생성 모델링의 경우, 단순히 data \(x\)가 conditioning 정보 \(c\)와 함께 입력으로 들어간다는 점이다. 즉, reverse process에서 \(\epsilon_\theta\)가 \(\epsilon_\theta (z_\lambda, c)\)로 바뀐다는 점이다.

3. GUIDANCE

GAN이나 flow-based model의 경우 variance나 noise input의 범위를 줄여 diversity와 sample quality를 쉽게 trade-off 할 수 있다. 하지만 diffusion model의 경우 위와 같은 직관적인 접근은 효과적이지 않다.

3.1. CLASSIFIER GUIDANCE

truncation-like 효과를 얻기위해 ADM, 이전포스팅에서는 CG를 제안했다.

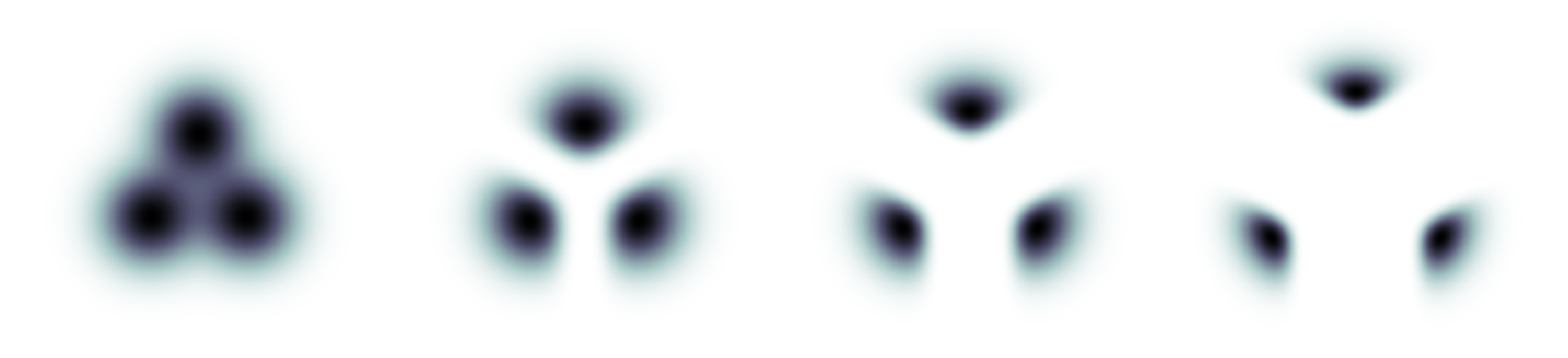The effect of guidance on a mixture of three Gaussians, each mixture component represent- ing data conditioned on a class.

위 그림에서 오른쪽으로 갈수록 classifier guidance가 커질수록, guidance가 없을 때 Gaussian으로 분포하던 데이터들이 아주 좁은 영역으로 모이는 것을 확인할 수 있다.

Guidance weight를 \(w+1\)로 unconditional model에 적용하는 것은 이론적으로 \(w\)로 conditional model에 CG하는 것과 같지만, ADM 논문 실험 결과에서는 class-conditional model에 CG를 적용하는 것이 가장 좋은 결과를 냈으므로, 저자들은 이후 연구에서도 동일하게 conditional model을 guiding하였다고 한다.

3.2. CLASSIFIER-FREE GUIDANCE

저자들이 제안한 CFG는 \(\epsilon_\theta (z_\lambda, c)\)를 수정하여, classifier없이 CG와 같은 효과를 낼 수 있다고 한다.

Training: 별도의 classifier를 학습하는 것이 아니라, unconditional diffusion model(\(p_\theta(z)\))과 conditional diffusion model(\(p_\theta(z \vert c)\))를 함께 학습 시킨다. 하나의 NN을 사용하여 구현할 수 있으며 hyperparameter \(p_\textrm{uncond}\)를 정해 특정 확률로 null token이 condition으로 입력되는 것이다.

Sampling: conditional model과 unconditional model의 선형 결합으로 추정한다.

\[\begin{equation} \tilde{\epsilon}_\theta (z_\lambda, c) = (1 + w) \epsilon_\theta (z_\lambda, c) - w \epsilon_\theta (z_\lambda) \end{equation}\]

4. EXPERIMENTS

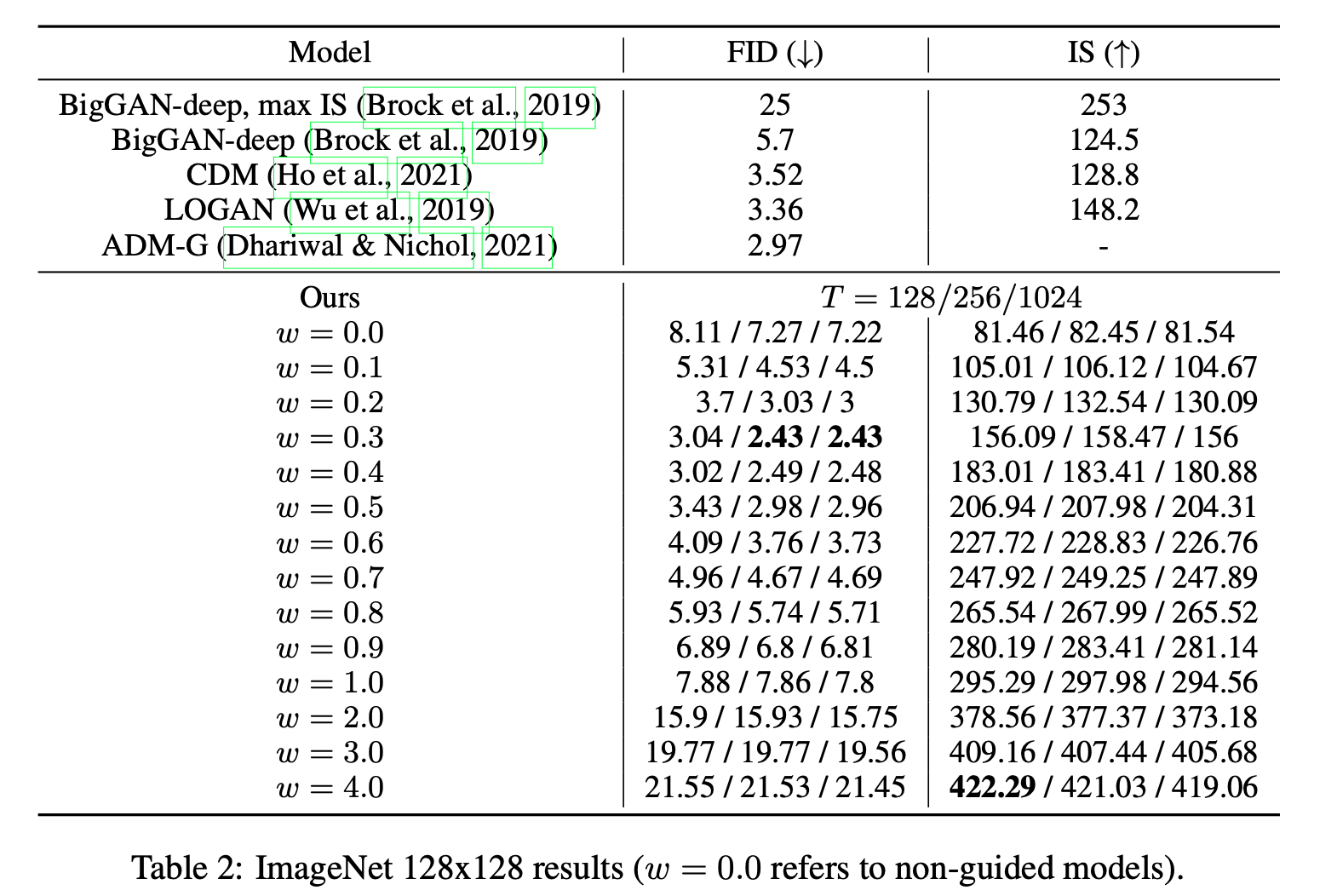
저자들의 목표는 CFG도 CG처럼 FID/IS trade-off를 달성할 수 있을지이다.(SOTA 수준의 Sample quality를 얻기 위함이 아니라) 그렇기 때문에 ADM의 model 구조나 hyper parameter를 그대로 사용하였다고 한다.

이때 저자들은 추가적인 classifier를 사용하지 않아 더 적은 model capacity를 사용하면서, ADM과 비슷하거나 때로는 더 높은 품질의 이미지를 생성했다고 한다.

4.1. VARYING THE CLASSIFIER-FREE GUIDANCE STRENGTH

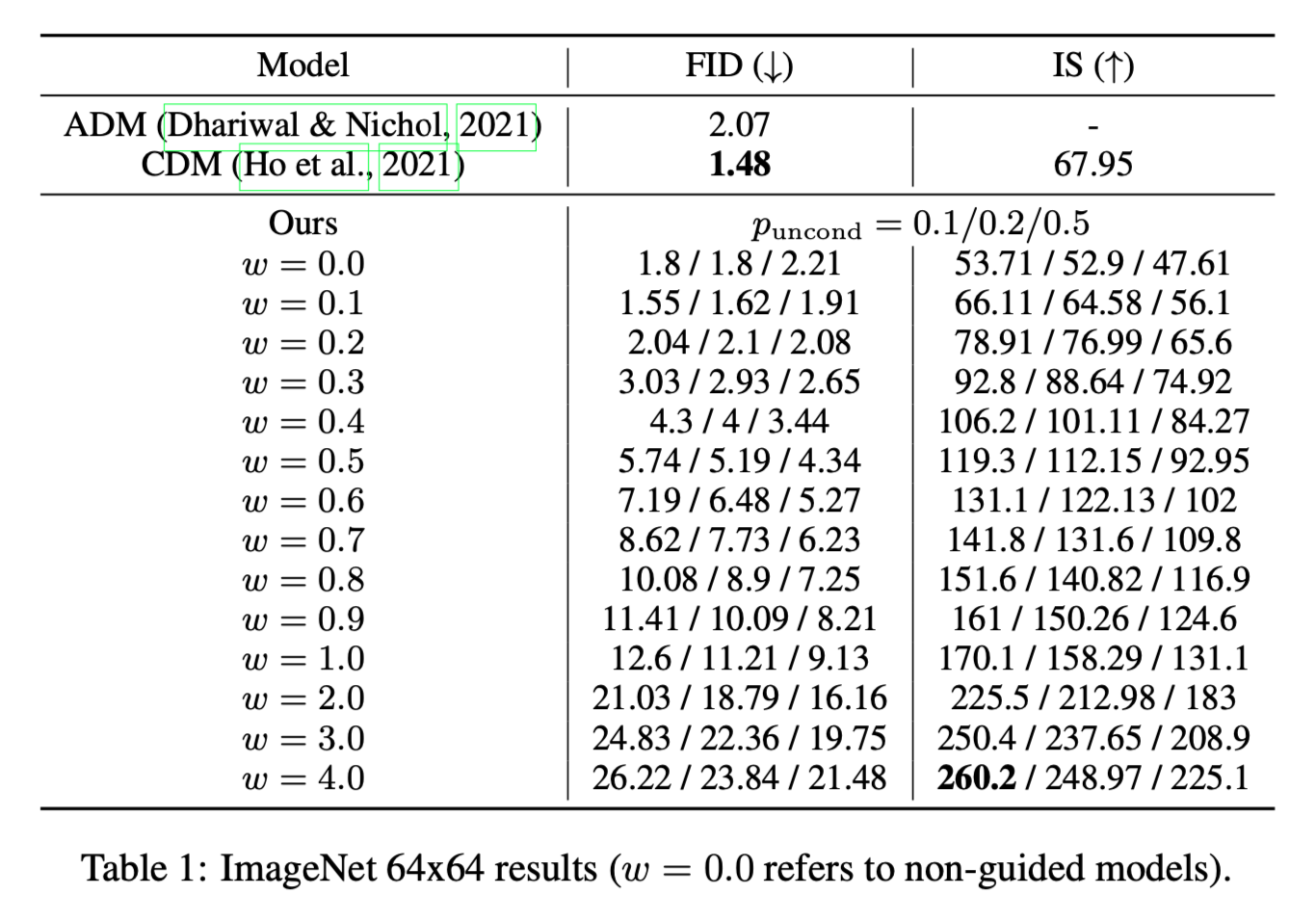
저자들은 본 논문의 메인 목표인 Guidance strength를 바꿔가며, IS와 FID score를 trade-off 할 수 있는지 실험하였다. \(64 \times 64\), \(128 \times 128\) 크기의 class conditional ImageNet generation으로 실험을 진행하였다.

(당연하게도) 실험 결과 CG와 같이, CFG에서도 IS와 FID score를 trade-off할 수 있었다.

4.2. VARYING THE UNCONDITIONAL TRAINING PROBABILITY

저자들은 Main hyperparameter인 \(p_\textrm{uncond}\)의 영향을 알아보기 위해 \(64 \times 64\) 크기의 ImageNet dataset을 이용하여 실험을 진행하였다.

실험 결과 \(p_\textrm{uncond}\)가 \(0.1\), \(0.2\)일 때 성능이 좋았다고 한다. 흥미롭게도 CG의 경우 상대적으로 작은 classifier가 CG에 충분하다고 하는데, 이는 저자들의 CFG와도 같은 결과라는 점이다.

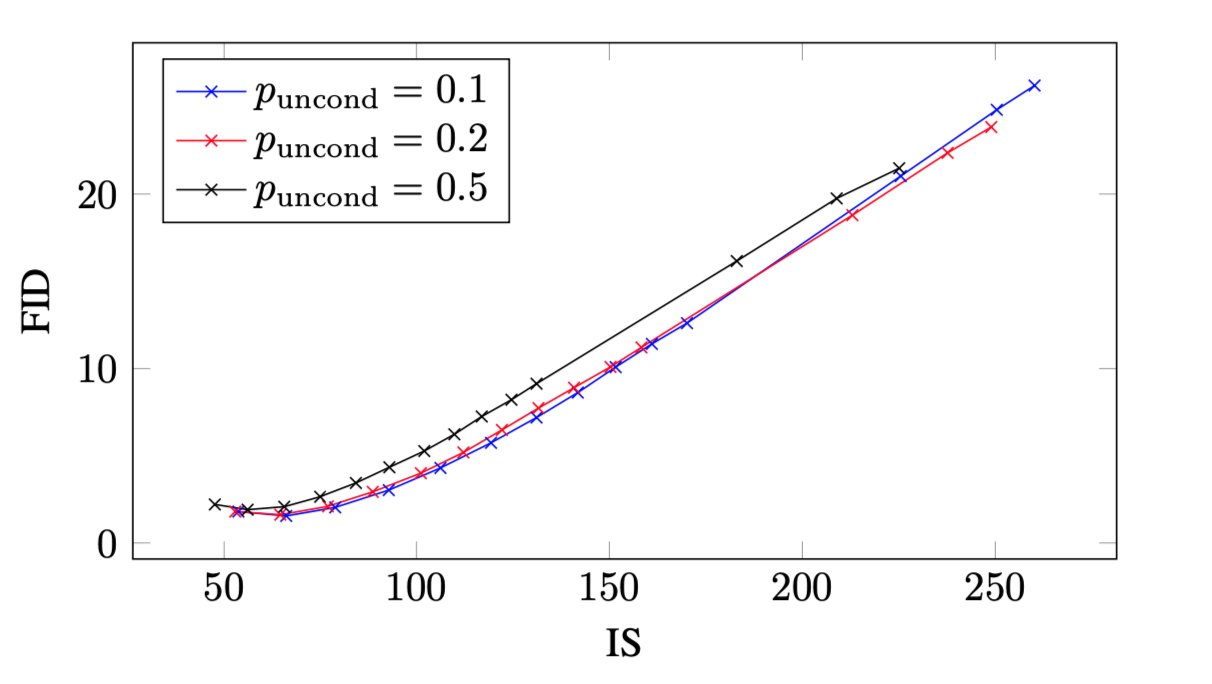
4.3. VARYING THE NUMBER OF SAMPLING STEPS

Diffusion model에서 sampling step은 이미지 품질에 주된 영향을 미치는 요인이다.

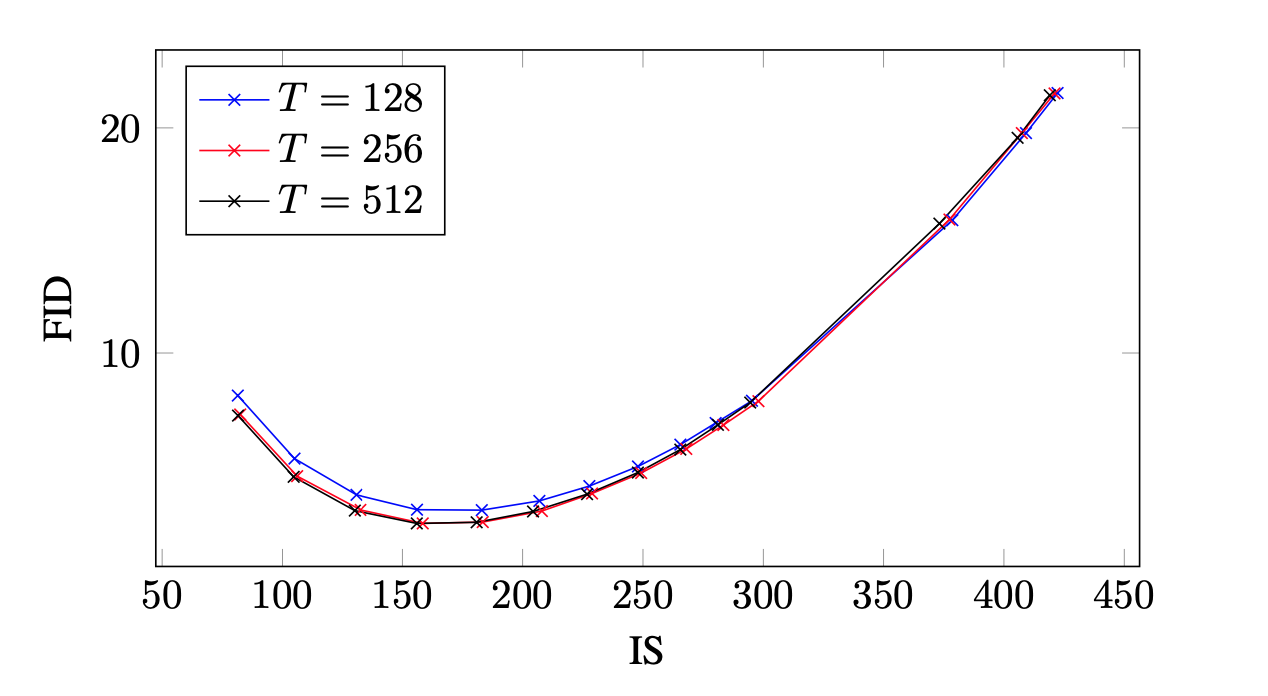IS/FID curves over guidance strengths for ImageNet 128x128 models. Each curve represents sampling with a different number of timesteps T

실험 결과 \(T = 256\)이 sampling time과 sample quality를 모두 고려했을 때 적절했다고 한다. 하지만 저자들의 모델에서는 한 step당 denoising과정을 두 번(conditional, unconditional)거치기 때문에 비슷한 계산량의 ADM-G (\(T= 256\))과 비교하려면 CFG(\(T = 128\))의 FID score가 underperform한다고 한다.

5. DISCUSSION

CFG의 장점은 매우 간단하다는 점이다. 코드 한 줄만 추가하면 된다.

• training시 conditioning을 randomly drop out
• sampling시 conditional과 unconditional score estimate를 mix

Guidance가 어떻게 작동하는지 직관적인 설명이 가능하다. unconditional의 likelihood를 감소시키고, conditional의 likelihood를 증가시키는 방향으로 동작한다는 것이다. 이는 다른 분야에서도 적용될 수 있다.

다만 CFG의 가장 큰 단점은 conditional, unconditional 두 개의 path를 통과해야 하기 때문에 denoising step이 비슷한 크기의 모델에 비해 2배 정도 느리다는 점이다.

마지막으로 저자들은 샘플 다양성을 희생하면서 샘플 품질을 올리는 것이 적합한지에 대해 의문을 던진다. 따라서 샘플의 품질을 증가시키면서 다양성을 유지하는 향후 연구가 필요하다고 한다.

Reference

JiYeop Kim’s blog를 참고하여 작성하였습니다.