[Study] Diffsion Basic

Diffusion Model Basic

Computer Vision 분야의 Generative model로 2020년부터 주목받고 있는 Diffusion Model에 대한 설명입니다. Diffusion Model이 무엇인지 모르는 사람들도 읽을 수 있도록 작성했습니다.

이 포스팅은 Lil’Log와 Hugging face의 The Annotated Diffusion Model를 참고했습니다.

모델 수식에 대한 유도는 다음 포스팅에서 다루겠습니다!

TL;DR

Diffusion Model은 현재 이미지 생성 모델 분야에서 널리 쓰이는 모델입니다. 모델 학습에는 크게 두 가지 process이 있습니다.

1. Forward process 미리 정해진 noise scheduling에 따라 이미지에 noise를 추가해, noisy한 이미지를 만듭니다.

2. Reverse process Forward process의 역과정입니다. noisy한 이미지로부터, noise를 예측하고 제거하는 과정입니다. 모델은 이 과정을 학습합니다.

Reverse process를 적절히 학습한 모델은 완전한 noise로부터 여러 step의 reverse process를 거쳐 이미지를 생성하게 됩니다.

Diffusion model은 학습이 안정적이고 좋은 퀄리티의 이미지를 만들어낸다는 장점이 있지만, 이미지 생성에 많은 step(시간)이 걸린다는 단점이 있고, 더 빠른 이미지 생성을 위해 많은 연구가 진행 중입니다.

1. Introduction

Diffusion Model이란 non-equilibrium thermodynamics(Langevin dynamics)에 영감을 받아 고안된 모델입니다. 분자들이 진공에서 확산되는 것과 같이, Diffusion Model에서는 Markov chain을 정의해, 천천히 random noise가 원본 이미지에 더해지며(Forward Process) 서서히 noise한 이미지로 변하게 됩니다. 모델은 이렇게 noise가 더해져 가는 과정의 역과정(Reverse Process)을 적절히 예측하도록 학습됩니다.

모델이 적절히 학습된다면, 우리는 pure noise로부터 noise를 제거해나가며, 새로운 이미지를 얻을 수 있습니다.

말로만 이야기하면 어려우니 아래 그림을 보면서 이해해 봅시다.

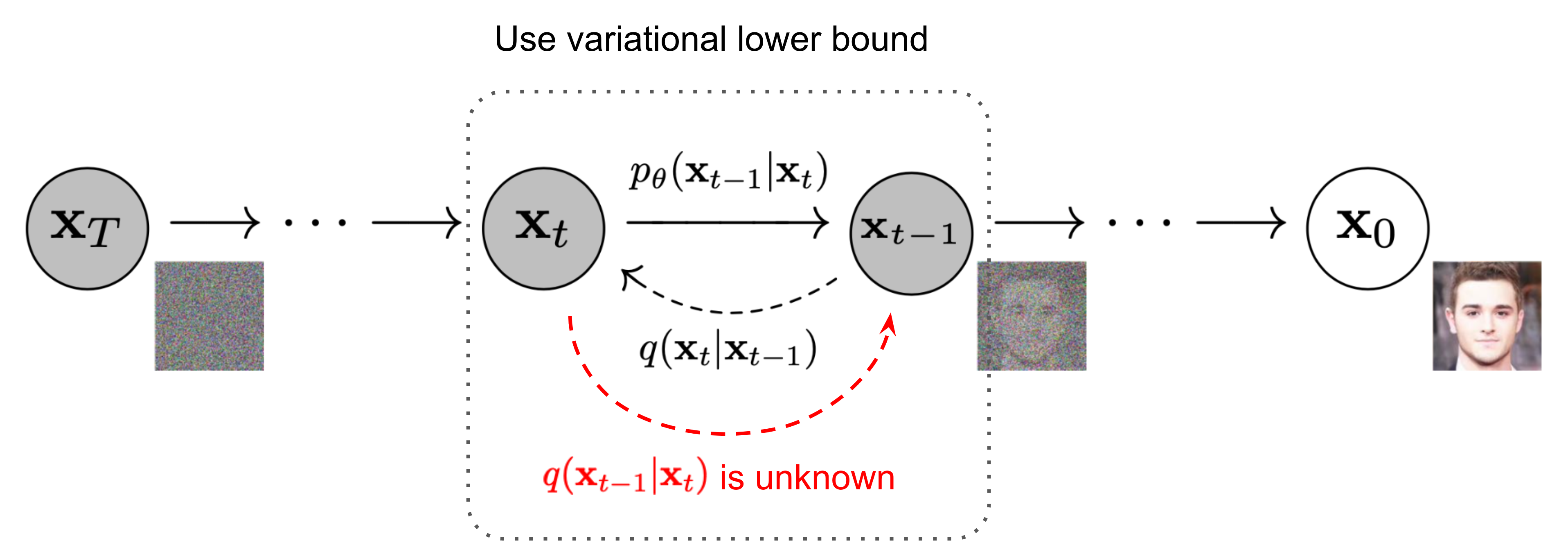_Fig1. The Markov chain of forward (reverse) process _

오른쪽 \(\mathbf x_{0}\)가 원본 이미지, 왼쪽 \(\mathbf x_{T}\)가 노이즈가 \(T\)번 추가되어, 완전한 노이즈 이미지(pure noise)로 변했다고 생각하면 됩니다.

Forward process, Reverse process, Sampling 과정을 살펴봅시다.

2. Forward diffusion Process

Forward process는 이전 스텝 이미지(\(\mathbf x_{t-1}\))에 time step 별로 정의된 (아주 작은) Gaussian Noise를 추가하는 과정입니다.

즉, 덜 noisy한 이미지에 noise를 추가해 noisy하게 만드는 과정을 총 \(T\)번 반복한다고 생각하시면 됩니다.

처음 Diffusion Model이 제안된 DDPM(Ho et al.) 에서는 \(T=1000\)을 사용했습니다.

Forward Process 를 수식으로 다음과 같이 나타낼 수 있습니다.

\[q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad\]

이때, reparamerization trick을 사용하면 (\(\alpha_t = 1 - \beta_t, \bar{\alpha}_t = \prod_{i=1}^t \alpha_i\)) 위 식은 다음과 같이 바꿀 수 있습니다. (유도 수식은 복잡하니 넘어가겠습니다.)

\[q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})\]

정리하자면, 원래 naive하게는 총 \(T\) 번동안 노이즈를 서서히 더해가면서 이미지를 서서히 noisy하게 만들어야 하지만, 위 process의 ‘Nice property’ 덕분에 원본 이미지 (\(\mathbf x_0\))로부터 임의의 time step (\(t\))의 이미지 (\(\mathbf x_t\))를 1번만에 sampling할 수 있습니다.

\[\begin{aligned} \mathbf{x}_t &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ \end{aligned}\] \[\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)\]

3. Reverse diffusion Process

다시 그림을 봅시다. 우리는 이전 forward process에서 이미지에 노이즈를 점점 더 해가는 과정, \(q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\)을 이해했습니다. (오른쪽에서 왼쪽으로 가는 화살표)

Reverse process란 이의 역 과정이라 생각하면 됩니다(왼쪽에서 오른쪽으로 가는 화살표). 현재 노이즈가 섞인 이미지를 보고, 1 step만큼 이미지를 제거하는 과정인 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\)가 Reverse process이며, 이를 안다면 우리는 pure Gaussian noise, \(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)로부터 원본 이미지를 생성해 낼 수 있음을 의미합니다. Forward process에서 작은 noise를 더했기 때문에 (\(\beta_t\)가 충분히 작으므로) \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\)도 Gaussian으로 근사할 수 있습니다.

하지만… 아쉽게도 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\)는 쉽게 추정할 수 없습니다. 따라서 우리는 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\)를 추정하도록 모델 파라미터 \(p_\theta\)를 모델이 학습하도록 목표를 바꿉니다.

\[p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\]

정리하자면, forward process에서 추가된 noise를 제거하는 과정을 reverse process라 하며, 이 과정도 Gaussian으로 근사할 수 있습니다. 따라서 Parameter를 모델이 학습하도록 \(p_\theta\)를 적절히 정의했는데… 그렇다면 \(p_\theta\)는 어떻게 학습이 되는 걸까요? 여기서부터는 수식이 많이 등장해 조금 복잡합니다.

4. Loss Function

Loss function은 VAE에서와 비슷하게 Variational Lower Bound (VLB)를 이용합니다. 수식 유도는 생략하고 결과만 나열하면 다음과 같습니다.

\[\text{Let }L_\text{VLB} = \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0)\]

\(L_\text{VLB}\)를 열심히 정리하면, 여러개의 KL-divergence term과 entropy term으로 나타낼 수 있습니다. 이 역시 수식은 생략하고 결과만 보겠습니다.

\[\begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ \vdots \\ &= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned}\]

간단히 요약하면 다음과 같습니다.

\[\begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned}\]

여기서 \(L_T\)는 상수이므로, training에서 고려할 필요가 없습니다.

\(q\)는 learnable parameters가 없으며, \(\mathbf x_{T}\)는 Gaussian noise이므로, 학습에서 제외합니다.

또한 \(L_0\)역시, Ho et al. 2020에서 discrete decoder를 이용해 modeling 합니다.

따라서 우리가 주목해야 할 것은 \(L_t \text{ for }1 \leq t \leq T-1\) 입니다. 다음에서는 이 \(L_t\)를 어떻게 parameterization하는지 자세히 살펴보겠습니다.

5. Parameterization of \(L_t\) for Training Loss

자 위 내용을 정리해봅시다.

• 우리의 목적은 Reverse process, \(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\)를 학습하는 것이다.
• 이때, Loss function 은 VLB를 이용해 나타낼 수 있다.
• 이를 정리하면 여러개의 KL-Divergence로 나타낼 수 있는데 이 중 우리가 주목할 것은 \(L_t\)이다.

5.1 \(\tilde{\boldsymbol{\mu}}_t\)

Reverse process에서 주목해야할 것은, 만약 원본 이미지가 주어진다면, reverse conditional process는 tractable하다는 것입니다.

\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I})\) 이를 Bayes’ rule를 이용해 열심히 계산하면(역시 굳이 알 필요 없습니다), 다음을 얻습니다. 이때 위에서 언급한 ‘Nice property’를 이용합니다. (\(\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)\))

\[\begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\ &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{aligned}\]

5.2 \(L_t\)

Reverse process, \(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\)는 \(\boldsymbol{\mu}_\theta\)가 \(\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)\)를 예측하도록 학습하게 됩니다.

이때, \(\mathbf x_t\)는 training time에서 입력으로서 알 수 있으며, \(\alpha_t\)또한 미리 정의한 값이므로, 우리는 \(\boldsymbol{\epsilon}_t\)를 예측하는 것으로 reparameterize하여 표현할 수 있습니다.

\(\boldsymbol{\epsilon}_t\)를 예측하도록 하는 것이, \(\tilde{\boldsymbol{\mu}}_t\)를 직접 예측하도록 하는 것보다 성능이 좋다는 것이 알려져 있습니다.

\[\begin{aligned} \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\ \text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \end{aligned}\]

따라서 이를 이용해 \(L_t\)를 정리하면 다음을 얻습니다.

\[\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}\]

5.3 \(L_{\text {simple}}\)

Diffusion Model을 처음 제안한, Ho et al. (2020)은 경험적으로 위 loss를 그대로 쓰는 것보다, simplified loss를 쓰는 것이 학습이 잘 되는 것을 확인했다고 한다. 즉, 앞에 있는 상수텀을 전부 무시하고, \(\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2\)만 남긴 \(L_t^\text{simple}\)을 제안합니다.

\[\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}\]

최종적인 알고리즘은 다음과 같습니다.

Fig2. The training and sampling algorithms in DDPM (Image source: Ho et al. 2020)

END…?

지금까지 Diffusion model에 대한 간단한(?) 설명이 담긴 포스팅이였습니다. 이번 포스팅에서 생략한 수식 이해와 관련한 부분도 열심히 정리해서 업로드하도록 하겠습니다. 긴 글 읽어주셔서 감사합니다 :)

Reference

Weng, Lilian. (Jul 2021). What are diffusion models? Lil’Log. https://lilianweng.github.io/posts/2021-07-11-diffusion-models/.

Denoising diffusion probabilistic models, Ho, Jonathan and Jain, Ajay and Abbeel, Pieter, 2020