[Paper Reivew] Diffusion Models Beat GANs on Image Synthesis (ADM)

NIPS 2022. [Paper] [Github]
Prafulla Dhariwal, Alex Nichol, OpenAI
1 Jun 2021

들어가며

이 포스팅은 OpenAI에서 발표한 Diffusion Models Beat GANs on Image Synthesis를 읽고 공부한 내용을 담았습니다.

잘못된 내용이 있다면 댓글로 알려주세요 !

1. Introduction

Diffusion 기반의 모델들이 놀라운 성능을 보여주고는 있지만 위 논문이 발표되기 전까지, 이미지 생성 분야에서는 GAN 기반 모델들이 SOTA를 달성하고 있었다. GAN 기반 모델은 likelihood-baed 모델에 비해 이미지의 품질은 높지만, 다양성이 작다는 점과 training이 힘들다는 문제가 지적되어 왔다.

이에 저자들은 GAN 기반 모델이 Diffusion 기반 모델보다 성능이 잘 나오는 이유가 아래 2가지라고 가정한다.

1. GAN 기반 모델은 여러 연구들을 통해 모델 구조가 정제되고 탐구되어 왔다.
2. GAN 기반 모델들은 fidelity와 diversity가 trade-off가 가능하다. 이에 따라 GAN 기반 모델들은 diversity를 희생하여 high quality의 이미지를 생성하였다.

저자들은 이러한 GAN의 장점을 Diffusion model에 가져오려는 시도를 하였다. 먼저 model architecture를 다양한 ablation을 통해 개선하였고, fidelity와 diversity를 trade-off하려는 방법을 고안하였다.

이러한 과정을 통해 저자들은 여러가지 metric과 dataset에서 GAN을 능가하는 새로운 SOTA 성능을 달성할 수 있었다.

2. Background

이 절에서는 DDPM (Ho et al.)과 IDDPM (Nichol and Dhariwal), DDIM (Song et al)의 간단한 설명과 결론을 제시한다.

먼저 DDPM의 경우 high level에서 보면, noisy한 이미지 \(x_t\)로부터, 노이즈를 제거한 \(x_{t-1}\)를 예측하는 모델이다. 이때, \(x_{t-1}\)를 직접 예측하는 것보다 reparameterization trick을 사용하여, 노이즈 \(\epsilon_\theta (x_t, t)\)를 예측하는 것이 효과적임을 확인하였다.

DDPM에서는 \(p_\theta (x_{t-1} \vert x_t)\)를 Gaussian distribution(\(\mathcal{N}(x_{t-1}; \mu_\theta (x_t, t), \Sigma_\theta(x_t, t))\))를 가정하며, 이때 평균 \(\mu_\theta(x_t, t)\)는 노이즈 \(\epsilon_\theta (x_t, t)\)로부터 계산할 수 있으며, 분산 \(\Sigma_\theta(x_t, t)\)는 상수(\(\beta_t\))로 가정한다.

2.1. Improvements

Nichol and Dhariwal는 DDPM에서 \(\Sigma_\theta(x_t, t)\)를 상수로 고정하는 것은 sub-optimal하다고 주장하며, 이 값을 parameterize해야 한다고 주장하였다.

\[\begin{equation} \Sigma_\theta (x_t, t) = \exp (v \log \beta_t + (1-v) \log \tilde{\beta}_t) \end{equation}\]

또한 IDDPM에서는 hybrid objective function을 제안했는데, \(\epsilon_\theta (x_t, t)\)와 \(\Sigma_\theta(x_t, t)\)를 모두 학습하기 위해 다음과 같은 objective function을 사용하였다. \(L_{\textrm{simple}} + \lambda L_{\textrm{vlb}}\)

마지막으로, Song et al. 은 DDIM을 제안하였는데, reverse noise를 변경하여, DDPM과 다른 reverse sampling이 가능하도록 했다. 이 noise를 0으로 설정하여, \(\epsilon_\theta (x_t, t)\)를 deterministic하게 mapping하면 50 step만으로도 높은 퀄리티의 이미지를 생성할 수 있었다고 한다.

3. Architecture Improvements

이 절에서 저자들은 다양한 ablation study를 진행하였다.

우선 기본적으로 DDPM은 UNet 구조를 사용한다. UNet에서는 Downsampling한 이후, 같은 해상도의 이미지를 skip connection으로 연결하며 Upsampling하는 과정을 거친다. 여기에 \(16 \times 16\) 크기의 feature map에서는 하나의 head를 가진 global attention layer를 적용한다.

여기에 저자들은 다음과 같은 구조 변화를 실험하였다.

1. model 사이즈를 유지하면서, depth/width 증가
2. Number of Attention head 증가
3. attention을 \(32\times 32\), \(16 \times 16\), \(8 \times 8\)과 같이 다양한 feature map에 적용
4. BigGAN residual block 사용
5. residual connection의 scale을 \(\frac{1}{\sqrt{2}}\)로 바꾸기

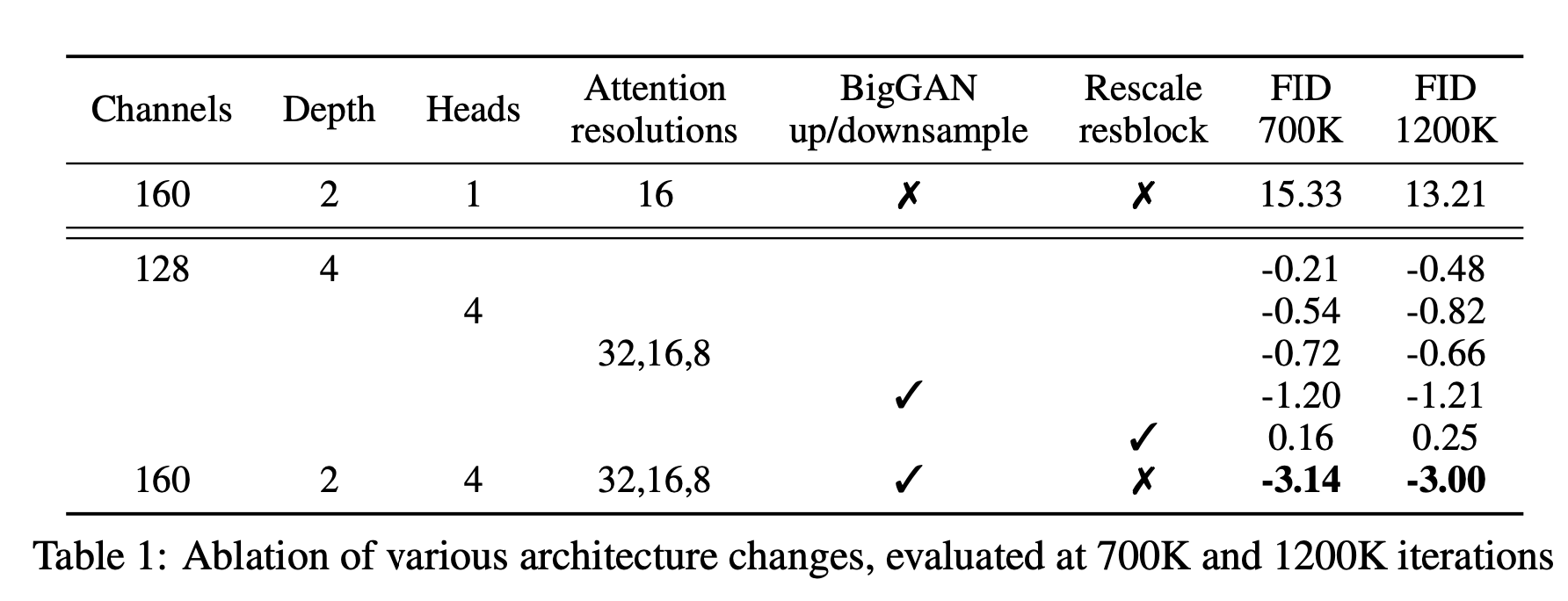Ablation of various architecture changes, evaluated at 700K and 1200K iterations

실험 결과 rescale resblock을 제외하고, 모두 FID score가 개선되는 것을 확인할 수 있었다.

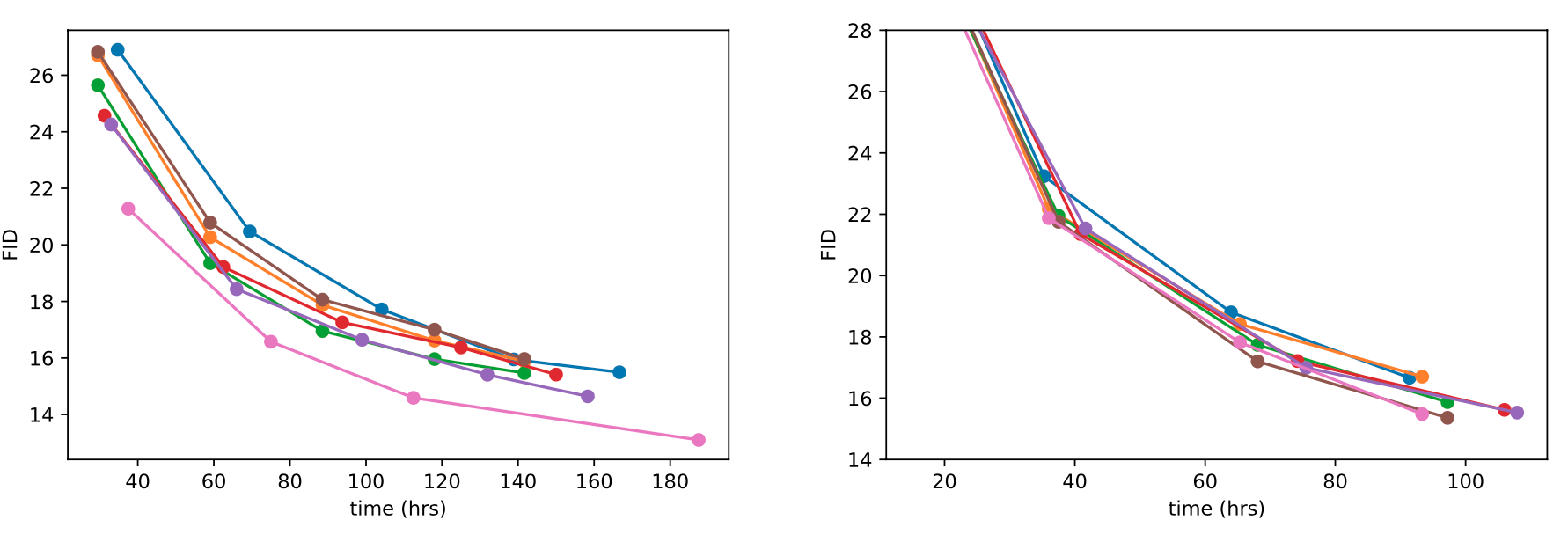Ablation of various architecture changes, showing FID as a function of wall-clock time.

또한 저자들은 위 그래프에서 볼 수 있듯이, depth를 늘리는 것은 perfomance 향상에 기여하기는 하지만, traning time이 너무 길어지기 때문에 앞으로의 연구에서는 사용하지 않았다고 한다.

3.1. Adaptive Group Normalization

저자들은 또한 Adaptive group Normalization (AdaGN) layer를 실험하였다. 이 layer에서는 group norm이후에, 각 residual block에서 timestep, class embedding을 결합한다. \(\begin{equation} \textrm{AdaGN}(h, y) = y_s \textrm{GroupNorm}(h) + y_b \end{equation}\) 이때 \(y = [y_s, y_b]\) 는 timestep, class embedding의 linear projection이다.

ablation 결과 AdaGN이 FID 개선에 효과적임을 확인하였다.

정리하자면 저자들은 이후 연구에서 다음과 같은 model architecture를 default로 사용한다고 한다.

1. Variable width with 2 residual blocks per resolution.
2. Multiple heads with 64 channels per head
3. Attention at 32, 16 and 8 resolutions
4. BigGAN residual blocks for up and downsampling
5. AdaGN for injecting timestep and class embeddings into residual blocks.

4. Classifier Guidance

잘 고안된 모델 구조를 사용하는 것에 이어, GAN은 class label을 많이 이용하여 conditional 이미지 생성을 한다. 이때

(1) class-conditional normalization statistics를 이용하거나,

(2) \(p(y \vert x)\) classifier 처럼 동작하는 discriminator를 이용한다.

class information이 중요하다는 것은 다른 연구에서도 자명하며, 심지어는 label이 제한적인 영역에서도 효과적이다. 저자들은 이미 AdaGN에서 class 정보를 embedding하였지만, classifier \(p(y \vert x)\)를 활용하여 diffusion generator의 성능을 향상하는 방법을 사용한다.

Sohl-Dickstein et al. and Song et al. 의 연구로부터 pre-trained diffusion model을 classifier의 gradient를 이용해 conditioning할 수 있다는 것이 알려져있다고 한다. 구체적으로, classifier \(p_\phi (y \vert x_t, t)\)를 noisy image \(x_t\)에 대해 학습시킨 뒤, \(\nabla_{x_t} \log p_\phi (y \vert x_t, t)\)를 이용하면 임의의 class label \(y\)를 diffusion process에서 conditioning할 수 있다는 것이다.

4.1. Conditional Reverse Noising Process

Unconditional reverse process로부터, class label \(y\)을 conditioning 하는 것은 다음과 같이 표현할 수 있다.

\[\begin{equation} p_{\theta,\phi} (x_t \vert x_{t+1}, y) = Z p_\theta (x_t \vert x_{t+1}) p_\phi (y \vert x_t) \end{equation}\]

일반적으로 분포는 intractable 하지만, Sohl-Dickstein et al은 perturbed Gaussian distribution으로 근사할 수 있음을 보였다. (이때 \(Z\)는 normalizing constant)

\[\begin{aligned} p_\theta (x_t | x_{t+1}) &= \mathcal{N} (\mu, \Sigma) \\ \log p_\theta (x_t | x_{t+1}) &= -\frac{1}{2} (x_t - \mu)^T \Sigma^{-1} (x_t - \mu) + C \end{aligned}\]

위 식을 열심히 전개하고 근사하고 정리하면,,,

\(\begin{aligned} \log (p_\theta (x_t \vert x_{t+1}) p_\phi (y \vert x_t)) & \approx -\frac{1}{2} (x_t - \mu)^T \Sigma^{-1} (x_t - \mu) + (x_t - \mu) g + C_2 \\ &= -\frac{1}{2} (x_t - \mu - \Sigma g)^T \Sigma^{-1} (x_t - \mu - \Sigma g) + \frac{1}{2} g^T \Sigma g + C_2 \\ &= -\frac{1}{2} (x_t - \mu - \Sigma g)^T \Sigma^{-1} (x_t - \mu - \Sigma g) + C_3 \\ &= \log p(z) + C_4, \quad z \sim \mathcal{N}(\mu + \Sigma g, \Sigma) \end{aligned}\) 다음과 같다고 한다.

정리하자면, conditional transition operator를 unconditional 과 유사하게 Gaussian 분포로 근사할 수 있는데, 이때 평균은 \(\Sigma g\) 만큼 이동하게 된다.

4.2. Conditional Sampling for DDIM

4.1 의 유도는 stochastic diffusion sampling에만 유효하며, DDIM 같이 deterministic한 방식에는 적용될 수 없다. 이에 저자들은 score-based conditioning trick을 채택한다. 만약 더해진 노이즈를 예측하는 모델 \(\epsilon_\theta(x_t)\)이 있는 경우, 다음과 같은 score function 유도가 가능하다.

\[\begin{equation} \nabla_{x_t} \log p_\theta (x_t) = - \frac{1}{\sqrt{1 - \overline{\alpha}_t}} \epsilon_\theta (x_t) \end{equation}\]

위 식을 \(p(x_t) p(y \vert x_t)\)에 대입하고 정리하면 다음과 같다.

\[\begin{aligned} \nabla_{x_t} \log (p_\theta (x_t) p_\phi (y | x_t)) &= \nabla_{x_t} \log p_\theta (x_t) + \nabla_{x_t} \log p_\phi (y | x_t) \\ &= - \frac{1}{\sqrt{1 - \overline{\alpha}_t}} \epsilon_\theta (x_t) + \nabla_{x_t} \log p_\phi (y | x_t) \end{aligned}\]

최종적으로, 새로운 노이즈 예측 \(\hat{\epsilon} (x_t)\)을 정의할 수 있으며, DDIM에서 사용한 것과 동일하지만 \(\epsilon_\theta (x_t)\) 대신 \(\hat{\epsilon} (x_t)\)만 사용하면 된다.

\[\begin{equation} \hat{\epsilon} (x_t) := \epsilon_\theta (x_t) - \sqrt{1-\overline{\alpha}_t} \nabla_{x_t} \log p_\phi (y | x_t) \end{equation}\]

4.3. Scaling Classifier Gradients

저자들은 실험 초기에 classifier scale 1.0을 사용했으나, 원하는 class의 이미지가 잘 생성되지 않았다. 이때 classifier scale을 10.0으로 키웠더니 아래와 같이 거의 100%로 원하는 class의 이미지를 생성해냈다고 한다.

classifier scaling의 효과는 다음 식으로부터 이해할 수 있다.

\[\begin{equation} s \cdot \nabla_x \log p (y | x) = \nabla_x \log \frac{1}{Z} p (y | x)^s \end{equation}\]

\(s > 1\)일 때, 분포는 \(p(y \vert x)\)보다 뾰족해지며, classifier의 mode에 초점을 맞추어, (덜 다양하지만) 높은 품질의 이미지를 생성하는데 적합하다.

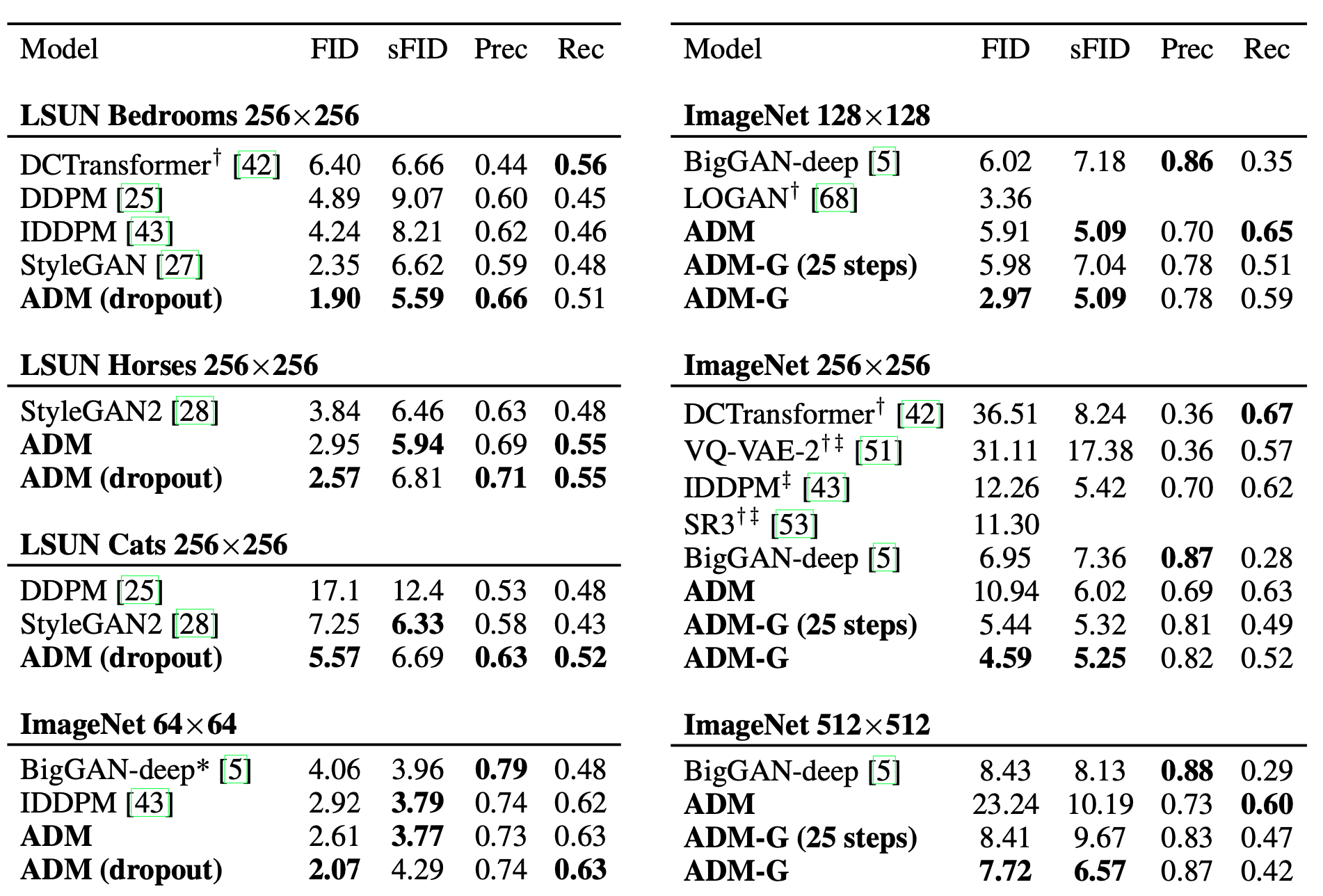
5. Results

6. Limitations and Future Work

Diffusion model은 이미지 생성 분야에서 매우 유망하지만 여전히 여러 단계의 denoising step을 거쳐야하므로, GAN에 비해 느리다는 점이 단점으로 꼽힌다.

또한 본 논문에서 제안된 classifier guidance technique은 labeled dataset에서만 사용할 수 있다. 아직 label이 없는 dataset에서 diversity와 fidelity사이 trade-off할 수 있는 방법이 고안되지 않았다.

classifier guidance의 효과는 classifier의 gradient로부터 강력한 생성 모델을 만들 수 있음을 시사한다. 이는 추후에 다양한 방법으로 pre-train 모델을 condition 할 수 있을 것이라 한다. 또한, 향후에는 대규모 라벨이 없는 데이터셋을 활용해 강력한 diffusion 모델을 사전 학습한 후, classifier를 사용해 이를 개선할 수 있는 가능성도 제시하고 있다.

7. Conclusion

저자들은 diffusion model이 GAN의 성능을 능가할 수 있음을 보였다. 개선된 모델 구조는 unconditional image generation 뿐만 아니라, classifier guidance technique을 활용해 class-conditioning도 가능했다. 또한 upsampling과 guidance를 결합하여, 샘플 품질을 더욱 향상 시킬 수 있었다고 한다.

Reference

JiYeop Kim’s blog를 참고하여 작성하였습니다.