[Paper Reivew] Improved Vector Quantized Diffusion Models (Improved VQ-Diffusion)
VQ-Diffusion이 갖는 문제를 Discrete Classifier-free Guidance, High-quality Inference Strategy을 이용해 개선한 연구입니다.
arXiv 2023. [Paper] [Github]
Zhicong Tang, Shuyang Gu, Jianmin Bao, Dong Chen, Fang Wen
Tsinghua University | University of Science and Technology of China | Microsoft Research 31 May 2022
TL;DR
기존 VQ-Diffusion(이전 포스팅)을 개선하여 더 좋은 성능을 얻은 연구입니다.
Prior외에도 posterior constraint를 더해 이미지 생성 품질을 높였습니다. 이때 저자들이 제시한 discrete classifier free guidance는 기존 classifier free guidance(CFG, 이전포스팅)보다 더 정확하고 일반적인 방법이라고 합니다.
High-quaility inference strategy를 도입하여, joint distribution issue를 해결했습니다.
1.Introduction
continuous diffusion model은 많은 연구가 진행되고 있지만, discrete diffusion model은 거의 연구가 진행되고 있지 않습니다. 이때 저자들은 discrete diffusion model의 대표적인 model인 VQ-Diffusion의 성능을 개선하는 것을 목표로하여 연구를 시작했다고 합니다.
Discrete classifier-free guidance.
Conditional image generation에서 diffusion model은 prior \(p(x \vert y)\)를 최대화하는 방향으로 학습하고, 이때 생성된 \(x\)는 posterior constraint \(p(y \vert x)\)를 만족할 것이라 가정합니다.
하지만 저자들은 이 가정이 틀릴 수 있으며, 많은 경우 posterior를 무시하게 된다고 합니다. 이 문제를 저자들은 posterior issue라고 명명했습니다. 이 문제를 해결하기 위해 저자들은 prior외에도 posterior를 동시에 고려하는 방법론을 제안합니다. 이 접근법은 Classifier free guidance(CFG)와 비슷하지만, 저자들의 방법은 노이즈가 아닌 확률을 예측하므로 더 정교하게 만들어진 방법이라고 합니다. 또한 CFG에서 input condition을 0으로 주는 것보다, \(p(x)\)를 추정하기 위해 학습 가능한 파라미터를 도입해 더 일반적이고 효과적이라고 주장합니다.
High-quality inference strategy.
기존 Reverse process에서는 여러 token을 동시에 샘플링하고, 독립적으로 확률을 추정합니다. 하지만 다른 구역이 사실은 의미적으로 연결되어 있을 수 있으며, 이는 독립적으로 확률을 추정하는 것은 이런 dependency를 무시하게 된다고 주장합니다. 저자들은 이 문제를 joint distribution issue라고 명명합니다.
이 문제를 해결하기 위해서, 저자들은 high-quality inference strategy를 제안합니다.
- Sample token 수를 줄입니다. (많은 token 수는 joint distribution issue를 야기합니다.)
- High confidence의 token이 더 정확하다는 것을 확인하고, 이를 위해 purity prior를 도입했습니다.
2. Background: VQ-Diffusion
이전 포스팅에서 자세하게 다뤘지만, 이번 포스팅에서도 간단하게 요약하겠습니다. (열심히 썼으니 한 번씩 읽어봐주세요)
VQ-Diffusion이란 VQ-VAE를 이용해 이미지 \(x\)를 discrete token \(x_0 \in \{1, 2, \cdots, K, K+1\}\)로 변환하는 것으로부터 시작합니다. 이때 \(K+1\)은 [MASK] token을 의미합니다.
forward process
\(q(x_t \vert x_{t-1})\)는 Markov chain으로 Gaussian noise를 조금씩 더해가는 과정으로 이해할 수 있으며, 다음과 같은 식으로 표현할 수 있습니다.
\[\begin{equation} q(x_t \vert x_{t-1}) = v^\top (x_t) Q_t v(x_{t-1}) \end{equation}\]이때 \(v(x)\)는 index \(x\)만 1인 one-hot column vector이고, \(Q_t\)는 \(x_{t-1}\)에서 \(x_t\)로의 transition matrix입니다.
\[\begin{equation} Q_t = \begin{bmatrix} \alpha_t + \beta_t & \beta_t & \beta_t & \cdots & 0 \\ \beta_t & \alpha_t + \beta_t & \beta_t & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \gamma_t & \gamma_t & \gamma_t & \cdots & 1 \end{bmatrix} \end{equation}\]\(\alpha_t \in [0,1], \beta_t = (1-\alpha_t) / K\) 이며, \(\gamma_t\)는 토큰이 [MASK] 토큰으로 교체될 확률을 의미합니다.
Reverse process
Reverse process는 posterior distribution으로부터 주어집니다. \(\begin{equation} q(x_{t-1} | x_t, x_0) = \frac{(v^\top (x_t) Q_t v(x_{t-1})) (v^\top (x_{t-1}) \overline{Q}_{t-1} v(x_0))}{v^\top (x_t) \overline{Q}_t v(x_0)} \end{equation}\)
이때, \(\overline{Q}_t = Q_t \cdots Q_1\)이며, cumulative transition matrix \(\overline{Q}_t\)와 \(q(x_t \vert x_0)\)는 다음과 같은 closed form으로 계산 가능합니다.
\[\begin{equation} \overline{Q}_t v(x_0) = \overline{\alpha}_t v(x_0) + (\overline{\gamma}_t - \overline{\beta}_t) v(K+1) + \overline{\beta}_t \\ (\overline{\alpha}_t = \prod_{i=1}^t \alpha_i, \overline{\gamma}_t = 1- \prod_{i=1}^t (1 - \gamma_i), \overline{\beta}_t = \frac{1 - \overline{\alpha}_t - \overline{\gamma}_t}{K}) \end{equation}\]VQ-Diffusion은 또한 reparameterization trick을 통해 각 step에서 noise가 아닌 denoised token distribution을 예측하도록 합니다.
\[\begin{equation} p_\theta (x_{t-1} | x_t, y) = \sum_{\tilde{x}_0 = 1}^K q(x_{t-1} | x_t, \tilde{x}_0) p_\theta (\tilde{x}_0 | x_t, y) \end{equation}\]하지만 저자들은 이런 VQ-Diffusion이 2가지 문제를 겪을 수 있다고 합니다.
Posterior issue : conditional image generation의 경우 conditional 정보 \(y\)를 denoising network에 직접 넣게 되는데, 이때 \(x_t\)에 충분한 정보를 갖고 있을 경우 \(y\)를 무시하는 경향이 있다고 합니다.
Joint distribution issue : time step, t에서 \(x_{t-1}\)의 각 location은 \(p_\theta(x_{t-1}\vert x_t)\)에서 독립적으로 샘플링되므로, 다른 위치에 있는 대응관계를 이용할 수 없는 문제가 발생한다고 합니다.
3. Method
3.1. Discrete Classifier-free Guidance
이전 VQ-Diffusion model은 text conditional 정보 \(y\)를 denoising network에 직접 주입하는 방식을 사용했지만, corrupted input이 일반적으로 텍스트보다 많은 정보를 가지고 있으므로, 모델은 텍스트 정보를 무시하는 경향이 있었다고 합니다.
Diffusion model은 \(p(x \vert y)\)를 최대화하는 방향으로 학습되지만, 높은 CLIP score를 위해서는 \(p(y \vert x)\)도 역시 최대화되어야 합니다. 직관적인 접근법은 \(\log p(x \vert y) + s \log p(y \vert x)\)를 최적화 하는 것입니다. Bayes’s theorem을 이용해 다음과 같이 정리할 수 있습니다.
\[\begin{aligned} & \underset{x}{\arg \max} [\log p(x|y) + s \log p(y|x)] \\ =& \underset{x}{\arg \max} [(s+1) \log p(x|y) - s \log \frac{p(x|y)}{p(y|x)}] \\ =& \underset{x}{\arg \max} [(s+1) \log p(x|y) - s \log \frac{p(x|y)p(y)}{p(y|x)}] \\ =& \underset{x}{\arg \max} [(s+1) \log p(x|y) - s \log p(x)] \\ =& \underset{x}{\arg \max} [\log p(x) + (s+1) (\log p(x|y) - \log p(x))] \\ \end{aligned}\]Unconditional image logit \(p(x)\)를 예측하기 위한 직관적인 방법은 GLIDE와 같이 일정 비율의 빈 조건(“null”)으로 Input을 주는 것입니다. 하지만 저자들은 “null”을 사용하는 것보다 학습 가능한 벡터를 사용하는 것이 logit \(p(x)\)를 예측하는데 도움이 되었다고 합니다.
Inference stage에서는 먼저 conditional image logit \(p_\theta (x_{t−1} \vert x_t, y)\)를 생성한 다음, conditional input을 학습 가능한 벡터로 설정함으로써 unconditional image logit \(p_\theta (x_{t−1} \vert x_t)\)를 예측하는 방향으로 진행됩니다.
\[\begin{equation} \log p_\theta (x_{t-1} | x_t, y) = \log p_\theta (x_{t-1} | x_t) + (s+1) (\log p_\theta (x_{t-1} | x_t, y) - \log p_\theta (x_{t-1} | x_t)) \end{equation}\]이전 CFG와 비교해서 저자들의 방법은 다음과 같은 차이점이 있습니다.
- VQ-Diffusion은 reparameterization trick을 사용해 노이즈가 없는 \(p(x \vert y)\)를 예측하므로, 다른 fast inference 전략들과 호환될 수 있습니다.
- Continuous diffusion model은 확률 \(p(x \vert y)\)를 직접 예측하지 않고, gradient를 이용해 근사하지만, Discrete diffusion model은 직접 예측할 수 있습니다.
- Continuous diffusion model은 \(p(x)\)를 예측하기 위해 “null” text를 사용하지만, Discrete diffusion model은 학습 가능한 벡터를 사용합니다.
3.2. High-quality Inference Strategy
VQ-Diffusion의 다른 문제는 다른 위치로부터의 Correlation을 무시한다는 것입니다. 이를 해결하기 위해 저자들은 두 가지 핵심 기법을 제안합니다.
Fewer tokens sampling.
저자들은 먼저 각 step에서 token수를 적게할 것을 제안합니다. 이렇게 함으로써 저자들은 다른 위치에 있는 토큰들을 독립적으로 샘플링 하는 대신, 반복적인 denoising step을 통해 위치간 correlation을 modeling 할 수 있었다고 합니다.
VQ-Diffusion의 각 step에서 변경되는 토큰 수는 불확실하지만, 간단한 설명을 위해 이를 변하지 않는 값이라고 가정합니다. 각 단계의 상태에서, 저자들은 [MASK]의 수를 계산하고, 이를 기반으로 적절한 timestep을 선택합니다. 입력 \(x_t\)에 대해 \(A_t := \{ i \vert x_t^i = [\text{MASK}]\}, B_t := \{ i \vert x_t^i \ne [\text{MASK}]\}\) 두 개의 집합으로 나눌 수 있습니다.
저자들의 목표는 각 step에서 \(A_t\)로부터 \(\Delta_z\)개의 [MASK] 토큰을 복구하는 것이라고 합니다. 따라서 전체 inference step은 \(T’ = (H \times W)/\Delta_z\)이며, 현재 time step은 다음과 같이 계산할 수 있다고 합니다. \(\begin{equation} \underset{t}{\arg \min} \| \frac{| A_t |}{H \times W} - \overline{\gamma}_t \|_2 \end{equation}\)
저자들이 제안한 fewer tokens sampling은 이전의 Fast sampling strategy와는 반대로 inference time의 희생을 통해 높은 품질의 이미지를 얻는 것을 목표로 한 것이라 합니다.
- 각 timestep \(t\)에 대해 [MASK] 토큰의 위치 \(i\)를 찾아 \(A_t\)에 저장합니다.
- \(A_t\)의 원소 중 \(\Delta_z\)개의 원소를 샘플링하여, \(C_t\)에 저장합니다.
- \(p_\theta (\tilde{x}_0 \vert x_t, y)\)에서 \(x_{0,t}\)를 샘플링하는데, 이는 \(p_\theta (x_{t-1} \vert x_t, y)\)에서 샘플링하는 것과 같다고 합니다.
- 이후 \(C_t\)의 원소에 대해서만 토큰을 교체합니다. (총 \(\Delta_z\)개의 토큰만 교체 대상)
- 이후 다음 timestep \(t\)를 계산합니다.
Purity prior sampling.
Lemma 1. \(x_t^i = [\text{MASK}]\)인 임의의 위치 \(i\)에 대하여, \(q(x_{t-1}^i = \text{[MASK]} \, \vert \, x_t^i = \text{MASK}, x_0^i) = \overline{\gamma}_{t-1} / \overline{\gamma}_t\)이다.
증명)
$$ x_t^i = [\text{MASK}] $$를 만족하는 위치 $$ i $$에 대하여, $$ \begin{aligned} & q(x_{t-1}^i = [\text{MASK}] \, | \, x_t^i = [\text{MASK}], x_0^i) \\ =& q(x_{t-1}^i = K+1 \, | \, x_t^i = K+1, x_0^i) \\ =& \frac{(v^\top (x_t^i) Q_t v(x_{t-1}^i))(v^\top (x_{t-1}^i) \overline{Q}_{t-1} v(x_0^i))}{v^\top (x_t^i) \overline{Q}_t v(x_0^i)} \\ =& \frac{(v^\top (K+1) Q_t v(K+1))(v^\top (K+1) \overline{Q}_{t-1} v(x_0^i))}{v^\top (K+1) \overline{Q}_t v(x_0^i)} \\ =& \frac{1 \cdot (v^\top (K+1) \overline{Q}_{t-1} v(x_0^i))}{v^\top (K+1) \overline{Q}_t v(x_0^i)} \\ =& \frac{v^\top (K+1) \overline{Q}_{t-1} v(x_0^i)}{v^\top (K+1) \overline{Q}_t v(x_0^i)} \end{aligned} $$ $$ x_0 $$가 noise가 없는 상태이기 때문에 $$ x_0^i \ne [\text{MASK}] $$임을 알 수 있다. 따라서 식을 정리하면 다음과 같다. $$ \begin{aligned} & q(x_{t-1}^i = [\text{MASK}] \, | \, x_t^i = [\text{MASK}], x_0^i) \\ =& \frac{v^\top (K+1) \overline{Q}_{t-1} v(x_0^i)}{v^\top (K+1) \overline{Q}_t v(x_0^i)} \\ =& \frac{\overline{\gamma}_{t-1}}{\overline{\gamma}_t} \end{aligned} $$
Lemma로부터 각 위치가 [MASK] state를 떠날 확률이 동일하다는 것을 보여줍니다. 즉, [MASK]로부터, non-[MASK]로 전이는 위치에 관계가 없다는 뜻입니다. 하지만 다른 위치에 따라 [MASK] 상태를 떠날 confidence는 다를 수 있습니다. 저자들은 purity score를 기반으로 샘플링을 수행했다고 합니다.
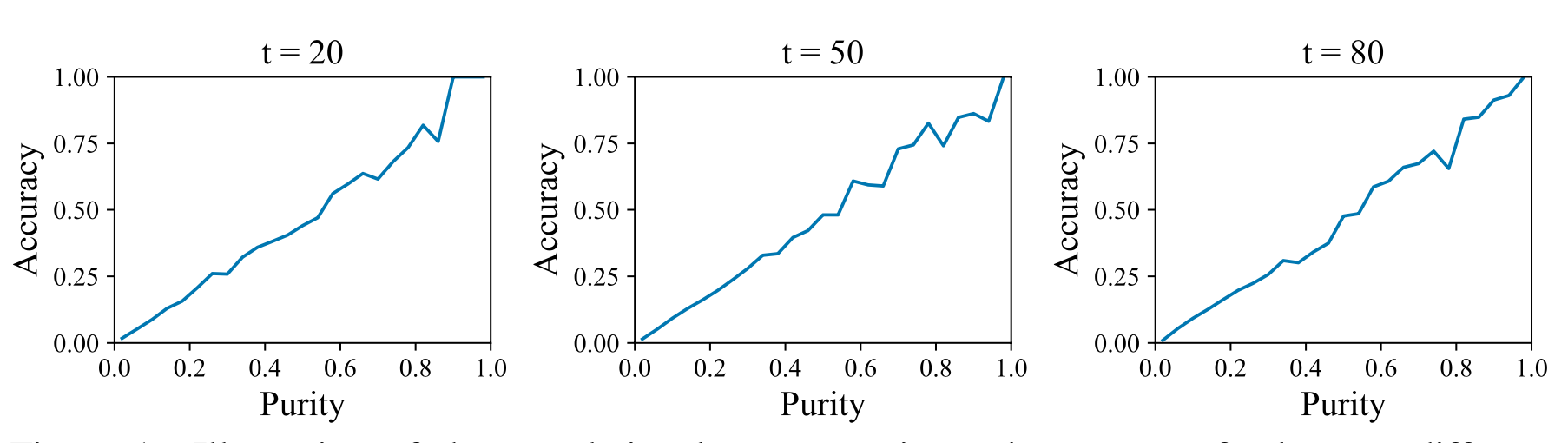Illustration of the correlation between purity and accuracy of tokens at different timesteps(t=20, 50, and 80). We find high purity usually yields high accuracy
purity prior를 이용해 저자들은 more confident region에서 샘플링을 할 수 있었으며, 이미지 생성 품질을 향상시킬 수 있었다고 합니다.
\[\begin{equation} purity(i, t) = \max_{j = 1 \cdots K} p(x_0^i = j | x_t^i) \end{equation}\]
Fewer token sampling과 비슷하지만, purity 계산을 통해, sampling 위치를 결정한다는 차이가 있습니다. 또한 purity가 높은 곳에서의 확률을 sharp하게 만드는 것이 이미지 품질 향상에 도움이 되므로, softmax 함수를 사용했습니다.
4. Experiments
4.1. Implementation details
Datasets
제안된 기술의 성능을 입증하기 위해, CUB-200, MSCOCO, Conceptual Captions(CC) 등 세 가지 텍스트-이미지 합성 데이터셋에서 실험을 수행했습니다.
CC 데이터셋에서는 균형 잡힌 서브셋을 사용하여 700만 개의 텍스트-이미지 쌍을 포함했습니다. 또한, 방법의 확장성을 입증하기 위해 인터넷에서 수집한 2억 개의 고품질 텍스트-이미지 쌍으로 이루어진 ITHQ-200M 데이터셋을 사용했습니다.
Backbone
Improved VQ-Diffusion-B (base): 3억 7천만(370M) 개의 파라미터를 포함하며, 원래 VQ-Diffusion의 네트워크 구조를 따르고, 공개된 모델을 사전 학습 모델로 사용한 후 각 데이터베이스에서 미세 조정을 수행했습니다.
Improved VQ-Diffusion-L (large): 12억 7천만 개(1.27B)의 파라미터를 포함하며, 이미지 디코더는 1408 차원의 36개 트랜스포머 블록으로 구성됩니다. 이 대형 모델은 ITHQ-200M 데이터셋에서 학습되었으며, 다른 데이터셋에서 베이스 크기 모델을 사용하여 대부분의 실험을 수행했습니다.
Evaluation metrics
- FID Score: 생성된 이미지의 품질과 다양성을 평가합니다.
- CLIP Score: 생성된 이미지와 텍스트 간의 유사성을 측정합니다.
- Quality Score QS): 이미지 품질만을 평가합니다.
- Diversity Score(DS): 생성된 이미지의 다양성을 측정합니다.
4.2. Ablation Studies
Discrete classifier-free guidance
저자들은 크게 4가지 setting에 대해 ablation study를 진행했습니다.
- Original VQ-Diffusion
- Classifier-Free Sampling: 추론 시 조건부 입력을 null 벡터로 설정하고, fine-tuning 없이 적용.
- Fine-Tuned Classifier-Free Guidance: fine-tuning 동안 10%의 조건부 입력을 null 벡터로 설정하고, 생성 시 Classifier-Free Guidance 적용.
- Learnable Vector for Unconditional Image: null 벡터 대신 학습 가능한 벡터를 사용하여 fine-tuning.
실험 결과 (당연하게도) 4번 실험 결과가 가장 좋았다고 합니다.
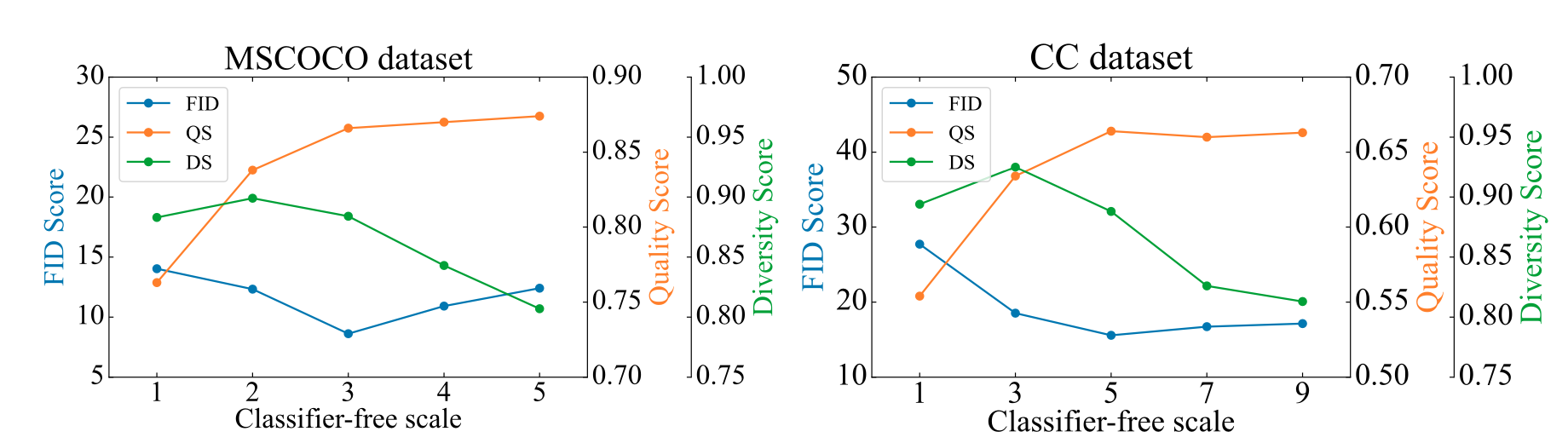
또한 저자들은 guidance scale \(s\)를 바꿔가면서도 실험을 진행한 결과, \(s\)를 키울수록 QS는 증가했지만, DS는 감소하는 경향이 있음을 확인했습니다.
High-quality inference strategy
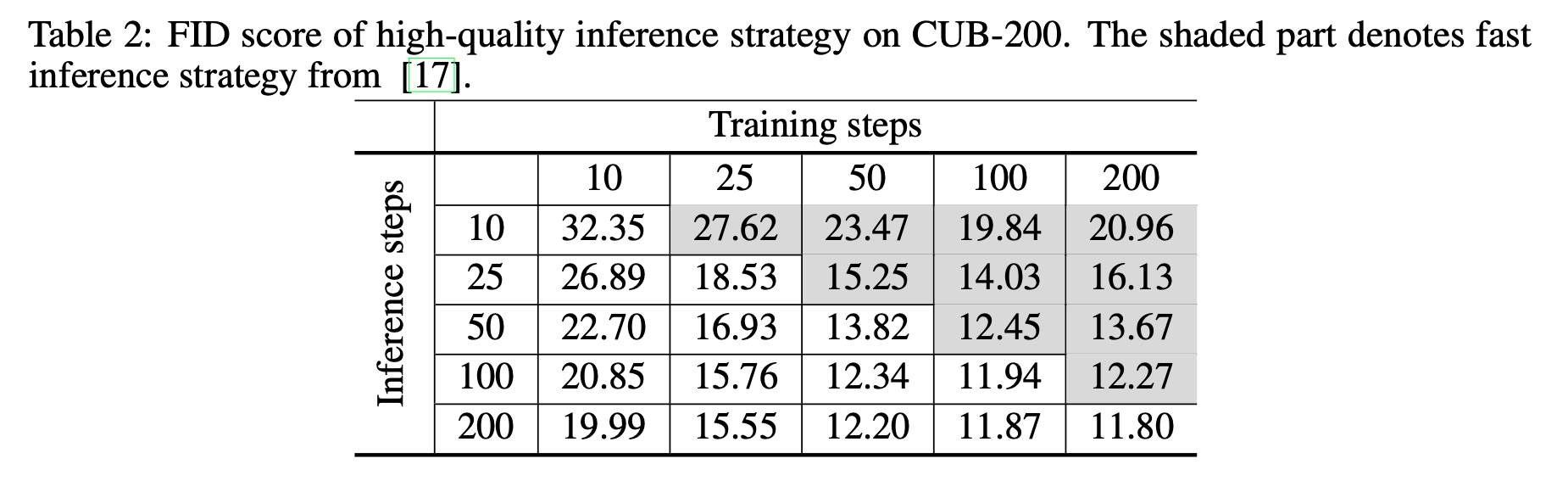
이전 연구들은 빠른 이미지 생성을 위해 학습에 사용한 것보다 적은 inference step을 이용해 이미지를 생성하는 방법론을 제시합니다. 하지만 저자들은 inference step을 늘려 이미지 품질을 향상 시키는 방법을 확인했다고 합니다. CUB-200 데이터셋에서 실험 수행하여, 25, 50, 100, 200 inference step에서 훈련된 모델의 성능 평가한 결과 inference step이 늘어날수록 더 좋은 FID score를 얻을 수 있었다고 합니다.
purity prior sampling
저자들은 Purity prior sampling이 이미지 생성 품질을 향상시킬 수 있는지 확인했습니다. MSCOCO, CUB-200, CC, ITHQ-200M 데이터셋에서 실험 수행했으며, 추가 훈련이나 추론 시간 없이 purity prior를 샘플링 과정에 통합했을 때 결과를 제시합니다.
실험 결과 purity prior를 통합하면 모든 dataset에서 성능이 향상되었다고 합니다.
Classifier-Free Guidance는 이미지 생성 시 품질과 다양성의 균형을 맞추는 데 효과적인 기술이지만, guidance scale sss와 같은 매개변수의 세심한 조정이 필요함.
High-quality inference strategy 전략은 추론 단계 수를 증가시킴으로써 이미지 품질을 크게 향상시킬 수 있음을 시사하며, 이는 속도보다 품질이 중요한 응용 프로그램에 적합.
Purity Prior Sampling은 대규모 데이터셋에서 이미지 생성 성능을 개선하는 간단하면서도 강력한 방법으로, 추가적인 훈련이나 추론 비용이 들지 않음.
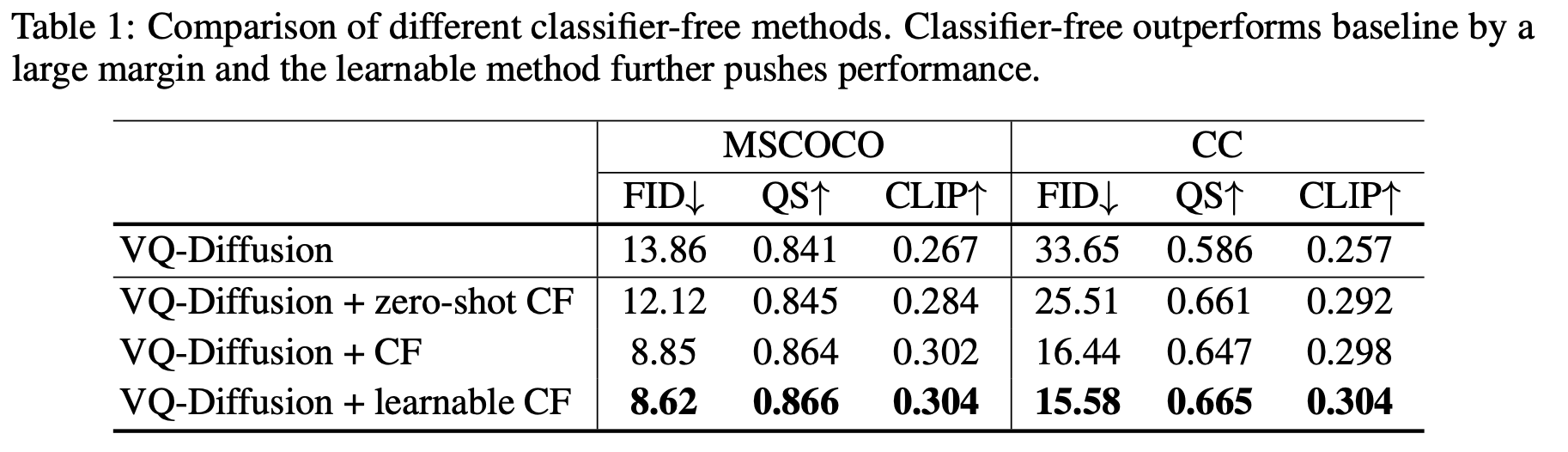
4.3. Compare with state-of-the-art methods
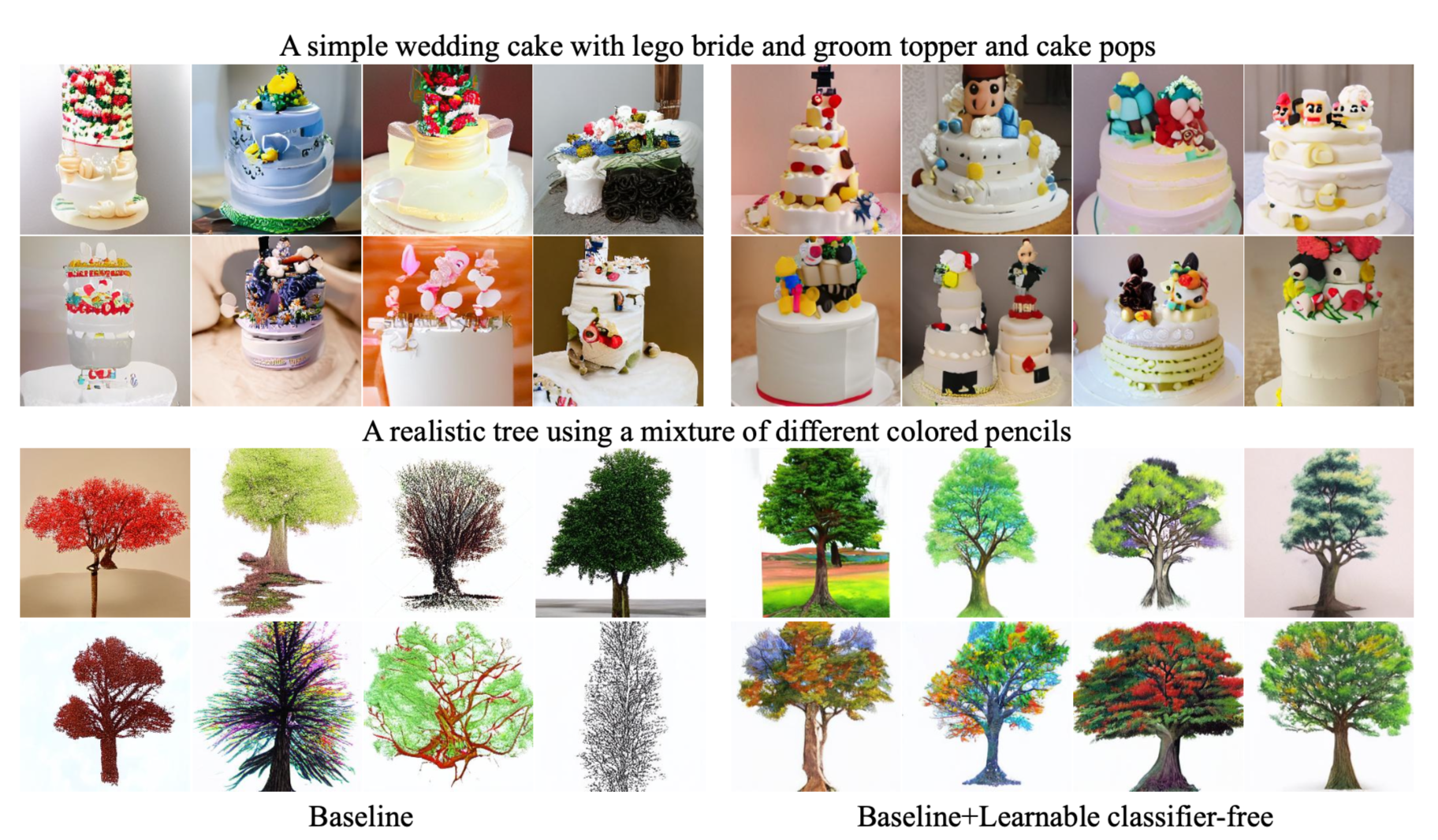
Zero-shot Classifier-Free Sampling과 고품질 추론 전략을 활용하여, 추가 훈련 없이 잘 훈련된 VQ-Diffusion 모델의 성능을 향상시켰으며, 모델을 학습 가능한 classifier-free 전략으로 fine-tuning할 경우, 성능이 더욱 개선되었다고 합니다.
5. Conclusion
이 논문에서는 VQ-Diffusion 모델의 두 가지 주요 문제, 즉 posterior issue와 joint distribution issue를 식별하고 이를 해결하기 위한 두 가지 기술(** Discrete Classifier-free Guidance, High-quality Inference Strategy**)을 제안했습니다. 이러한 기술을 통해 생성된 샘플의 품질과 입력 텍스트와의 일관성을 크게 개선했습니다.
- 핵심 성과:
- 제안된 전략은 모델을 fine-tuning하지 않고도 VQ-Diffusion의 성능을 향상시킬 수 있음.
- 다양한 데이터셋에서 제안된 방법의 우수성을 입증.
Reference
JiYeop Kim’s blog를 참고하여 작성하였습니다.