[Paper Reivew] Autoregressive Image Generation without Vector Quantization
Continuous-valued space로 AR 모델을 일반화하는 MAR 제안합니다.
NeurIPS 2024 (Spotlight). [Paper] [Github]
Tianhong Li, Yonglong Tian, He Li, Mingyang Deng, Kaiming He
MIT CSAIL | Google DeepMind | Tsinghua University
17 Jun 2024
TL;DR
Continuous-valued space로 AR 모델을 일반화하는 MAR 제안합니다. Diffusion model의 Condition을 AR 모델로 예측하고, 이를 Denoising 과정을 통해 multiple token을 동시에 예측.
1. Introduction
Autoregressive model들은 사실상 NLP 생성모델의 표준으로서, 언어의 discrete한 특성 때문에, model의 출력은 categorical, discrete-valued space.
이를 Continuous-valued space (e.g. image generation) 으로 일반화하려는 연구들이 있었지만, 대부분 Continuous 정보를 잘 discretize 하는데 초점을 맞추고 있었습니다. (가장 일반적인 방법은 image에 VQ를 통해 얻어진 유한한 크기의 vocabulary를 포함하는 discrete-valued tokenizer를 학습하는 것)
저자들은 한 가지 질문을 던집니다.
AR 모델이 꼭 VQ representation과 함께 사용되어야 할까?
AR 모델의 본질은 prefix를 가지고 next-token을 예측하는 것이지, 그 token이 discrete한지, continuous한 지는 관련이 없다는 것입니다.
이를 위해 필요한 것은 token 마다의 probability distribution 입니다. Discrete-valued 였을 때는 categorical로 표현하는게 편리해서지 필요해서가 아니라고 합니다. 만약 다른 방식으로 probability distribution를 표현할 수 있다면 VQ 없이 AR modeling을 할 수 있다고 합니다.
저자들은 continuous에서 동작하는 diffusion 과정을 통한 per-token probability distribution을 제안합니다. 특히 Denoising network의 condition으로 사용하는 \(z\)를 AR model을 이용해 예측하고, diffusion model로 arbitrary probability distribution을 표현하는 것입니다.
이런 방법론을 통해 discrete-valued tokenizer의 필요를 없애고, 이로 인해 발생했던 여러 문제들을 해결하며, 더 좋은 성능을 달성할 수 있었다고 합니다.
최종적으로 저자들은 randomized 순서로, multiple output 토큰들을 동시에 예측하는 masked generative model, MAR을 제안합니다.
저자들의 contribution을 요약하자면 다음과 같습니다.
- 기존 VQ tokenizer를 이용해 discrete하는 과정을 제거하고, continuous-value로 AR modeling
- MAR 모델링으로, multiple output token을 randomized 순서로 동시에 예측.
- 이미지 생성 품질 및 속도 개선
2. Related Work
Sequence Models for Image Generation
기존 많은 연구들은 discrete-valued token space에서 동작하는 tokenizer를 학습해 AR 모델링을 했으나, GIVT 에서는 Continuous-valued token을 이용하는 AR 모델링을 다뤘다고 합니다. GIVT 에서는 Gaussian mixture model을 사용했지만, 저자들은 diffusion process의 특징 덕분에 임의의 distirbution을 모두 모델링 할 수 있다고 합니다.
Diffusion for Representation Learning
Self-supervised learning의 criteria로서, diffusion process를 이용하는 연구들이 있습니다.
- DiffMAE : MAE의 \(\text{L}2\) loss를 denoising diffusion decoder로 교체
- DARL : denoising diffusion patch decoder와 AR 모델을 함께 학습.
이런 연구들은 representation 학습에 초점이 맞춰져 있지만, 저자들은 이미지 생성에 초점을 맞추고 있다고 합니다.
3. Method
저자들의 접근법은 VQ-VAE 처럼 quantized된 값이 아닌, continuous-valued tokenizer를 사용하는 sequence modeling입니다.
3.1. Rethinking Discrete-Valued Tokens
Discrete-valued token이 어떤 역할을 하는지 다시 생각해봅시다. Discrete tokenizer는 다음에 예측할 ground-truth token \(x\)를 integer로 표현할 수 있습니다. AR 모델은 continuous-valued \(D\)-dim vector \(z \in \mathbb{R}^D\)를 생성하고, 이후 \(K\)-way classifier로 projection 됩니다.
\[p(x | z) = \text{softmax}(Wz).\]Generative modeling 관점에서 probability distribution는 두 가지 특성을 보여야 합니다.
- Loss function 은 distribution간 거리를 측정할 수 있어야 합니다. (categorical distribution 에서는 cross-entropy)
- Sampler는 Inference time에서 \(x \sim p(x|z)\)로부터 sampling 할 수 있어야 합니다. categorical distribution 에서는 \(p(x | z) = \text{softmax}(Wz/\tau)\)에서 샘플링)
이 분석으로부터, 저자들은 다음의 결론을 얻습니다.
- AR modeling에서 discrete-valued token이 반드시 필요하지 않다는 것
- Token의 Distribution을 modeling하는 것이 중요!
3.2. Diffusion Loss
Diffusion model은 임의의 분포를 모델링하는 framework. 하지만 다른 일반적인 diffusion model(모든 픽셀이나 토큰의 joint representation을 모델링)과 다르게, 저자들은 각 token의 distribution을 표현하기 위해 diffusion model을 사용했다고 합니다.
즉 저자들은 continuous-valued vector \(x \in \mathbb{R}^d\)를 다음 위치에서 예측할 ground-truth token이라 할 때, AR 모델로 \(z \in \mathbb{R}^D\) 를 만들고, 이를 diffusion loss를 이용해 \(p(x|z)\)를 모델링 하고 싶은 것!
Loss function
저자들은 다음의 diffusion loss를 사용했습니다.
\[\mathcal{L}(z, x) = \mathbb{E}_{\epsilon, t} \left[ \| \epsilon - \epsilon_\theta(x_t | t, z) \|^2 \right].\]여기서 \(z\)는 AR에 의해 생성된 값이라는 것을 알고 있어야 합니다.
Sampler
Inference시 \(p(x|z)\) 에서 diffusion process를 거꾸로해서 sampling.
\[x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t | t, z) \right) + \sigma_t \delta.\]여기에 Temperature \(\tau\) 추가해서 sample diversity control 가능.
3.3. Diffusion Loss for Autoregressive Models
자… 다음으로 Diffusion Loss로 AR 모델을 표현해봅시다. Token sequence \(\{x^1, x^2, ..., x^n\}\) 가 주어졌을 때, AR 모델은 “next-token prediction” 방식으로 동작합니다.
\[p(x^1, \ldots, x^n) \prod_{i=1}^n p(x^i | x^1, \ldots, x^{i-1})\]저자들은 위 식을 두 part로 구분합니다.
- Conditioning vector, \(z^i = f(x^1, \ldots, x^{i-1})\)
- \(z^i\) 를 이용해 probability modeling \(p(x^i | z^i).\) 여기에서 Diffusion loss를 사용해서 backprop 과정을 통해 \(f(\cdot)\)학습.
3.4. Unifying Autoregressive and Masked Generative Models
저자들은 masked generative model (e.g. MaskGIT, MAGE)을 next token prediction concept으로 일반화 할 수 있다고 합니다.
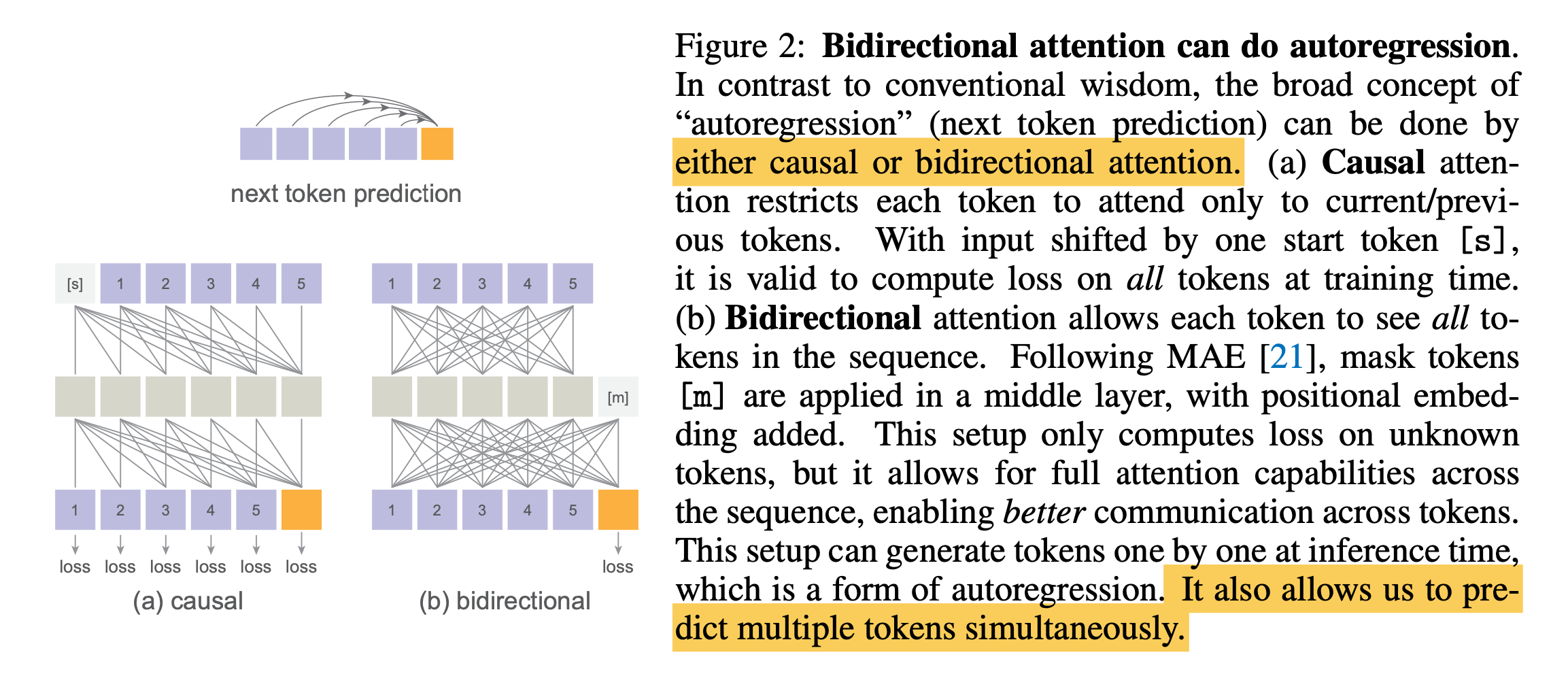
Bidirectional attention can perform autoregression
일반적으로 Transformer를 사용할 때, causal attention을 사용하지만, 저자들은 bidirectional attention으로도 구현할 수 있음을 보입니다.
Fig2-(b)와 같이 MAE 처럼 bidirectional attention을 하기 위해
- Known token(+P.E) 에 대해 MAE-style encoder를 태웁니다.
- Masked token(+P.E)를 Concat.
- 이를 MAE-style decoder에 mapping.
이때 Loss는 causal attention과는 다르게 unkown token에 대해서만 계산합니다.
이런 MAE-style trick으로 모든 토큰이 서로를 볼 수 있게, 모든 unkown token이 known token을 볼 수 있게 합니다. Inference시에는 AR의 형태로 bidirectional하게 token을 생성합니다. 이런 full attention은 생성 퀄리티를 높이며, 더 명확한 speed-accuracy trade-off 관계를 가진다고 합니다.
Autoregressive models in random orders
Masked generative model과 같이 저자들은 random하게 token 예측 순서를 바꾼다고 합니다. (Figure 3 - (b)). 이후 원래 위치 정보를 가지고 있는 P.E. 를 decoder layer에 더해주어 위치에 대한 정보를 제공합니다.
Masked autoregressive models
하나의 토큰만 예측하는 것이 아니라 여러개의 토큰을 예측하도록 할 수 있습니다. (Figure 3 - (c)).
| $$ p({x^i, x^{i+1}, \ldots, x^j} | x^1, \ldots, x^{i-1}) $$로 표현할 수 있는데, 다음과 같이 바꿔쓸 수 있습니다. |
여기서 \(X^k\)는 \(k\)-th step까지 예측한 token의 집합입니다.
여기서 저자들은 next set-of-tokens prediction을 AR 모델의 일반화 된 형태라 보고 Masked Autoregressive Model, MAR이라 부릅니다.
MAR은 개념적으로 MAGE (혹은 MaskGIT)과 관련이 있다고 합니다. 하지만, MAR은 각 token의 probability distribution에 대해 \(\tau\)를 적용했지만, MAGE (혹은 MaskGIT)는 token location을 sampling할 때 \(\tau\)를 적용했다는 차이가 있다고 합니다. (결과적으로 완전히 randomized 하지 않으며, training-time and inference-time behavior의 커다란 차이를 야기함)
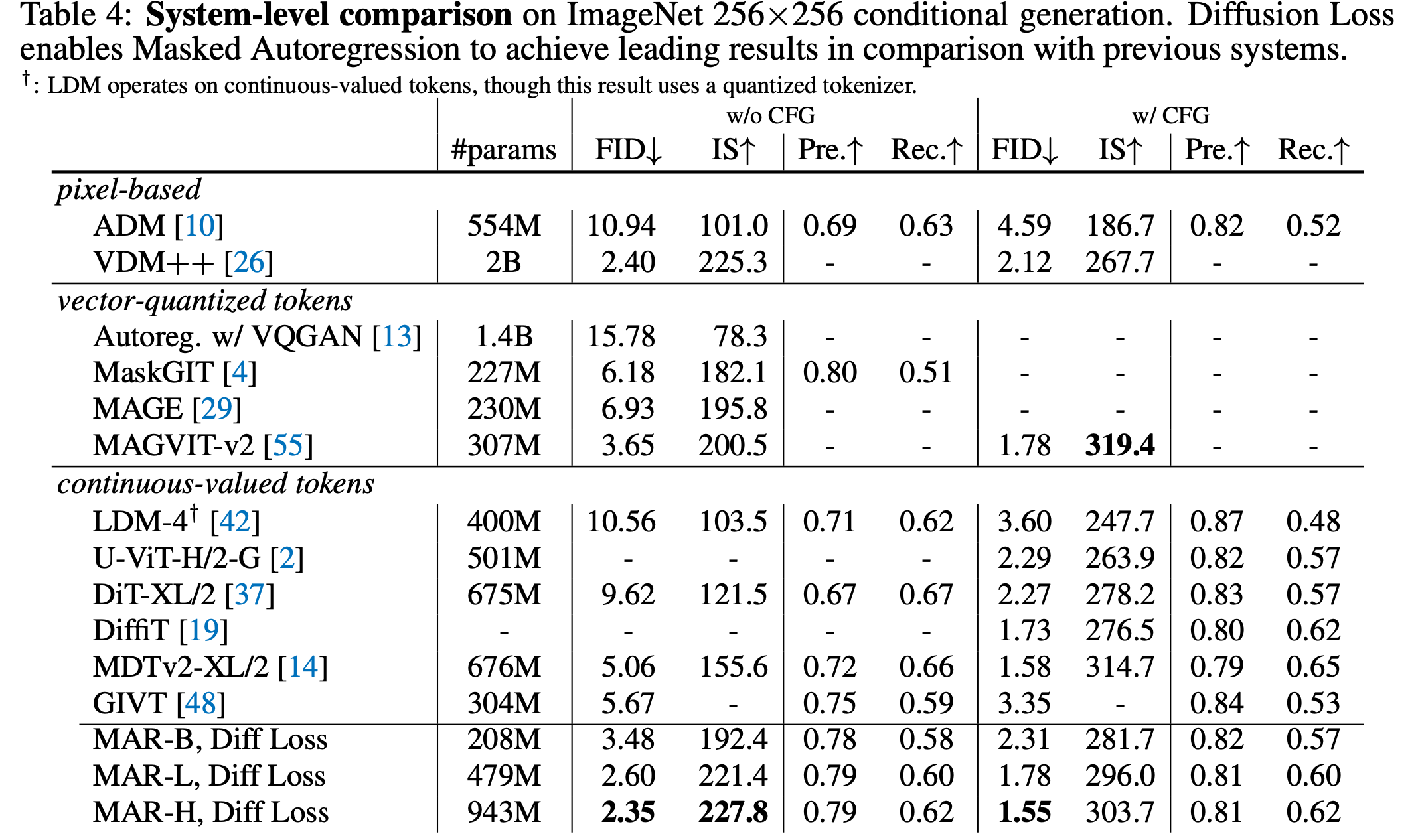
5. Experiments
- 데이터셋: ImageNet 256×256.
- 평가 지표: FID, IS, Precision, Recall.
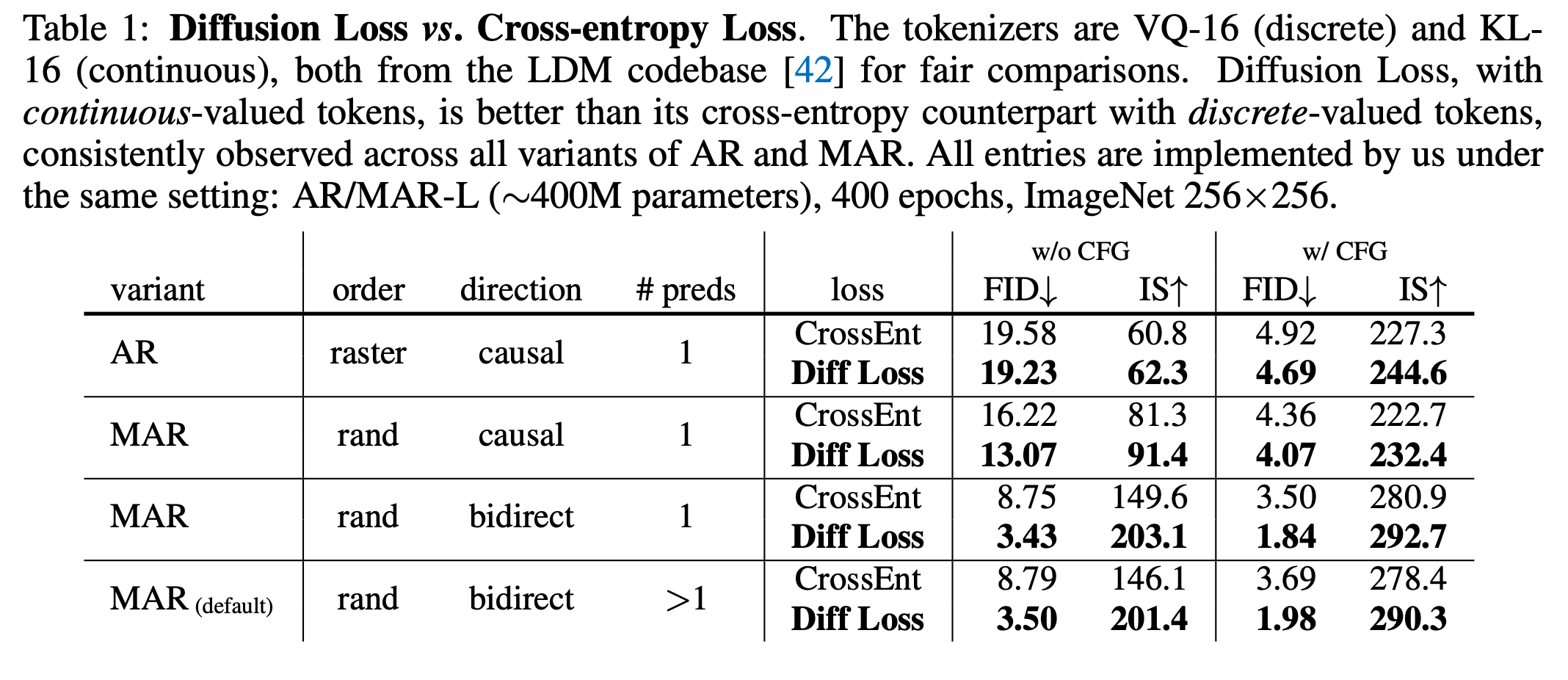
Diffusion Loss vs. Cross-entropy Loss
실험 결과 Diffusion Loss 가 일관적으로 cross-entropy의 성능을 능가했다고 합니다.
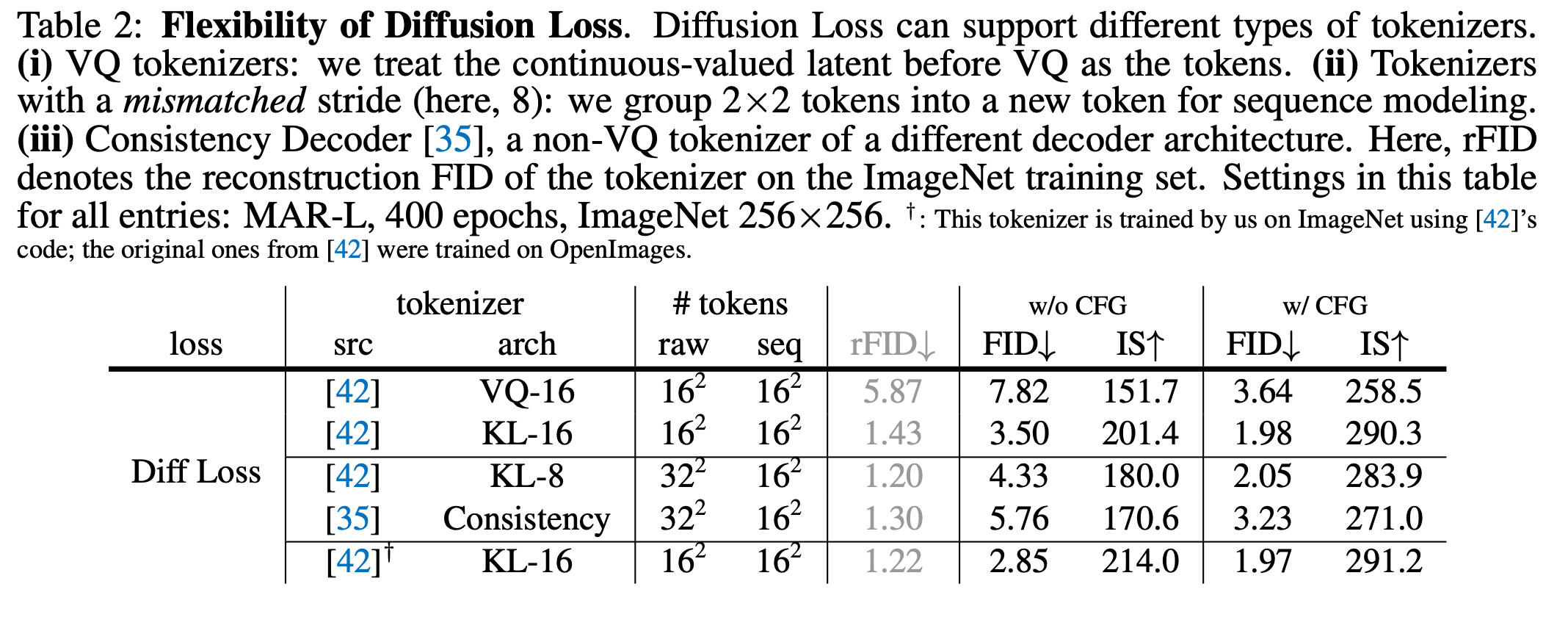
Flexibility of Diffusion Loss
Diffusion loss의 장점으로는 다양한 토크나이저와 호환이 가능하다는 점입니다. 동일한 VQ tokenizer cross entropy 사용 시 FID 8.79, Diffusion Loss 사용 시 FID 7.82 로 성능 개선.
VQ-16 vs. KL-16 비교: KL-16은 VQ-16 대비 재구성 FID(rFID)와 생성 FID에서 더 우수함(예: 7.82 vs. 3.50).
Stride가 다른 tokenizer도 처리 가능: KL-8 tokenizer(Strides: 8, 출력 길이: 32×32)를 사용하여 2×2 토큰을 그룹화해 2.05 FID 달성(KL-16의 1.98 FID와 유사).
Consistency Decoder 같은 non-VQ tokenizer도 가능.
Denoising MLP in Diffusion Loss
작은 MLP(2M 파라미터)도 경쟁력 있는 결과를 제공.
Sampling Steps of Diffusion Loss
100 step으로도 강력한 생성 품질을 달성 가능.
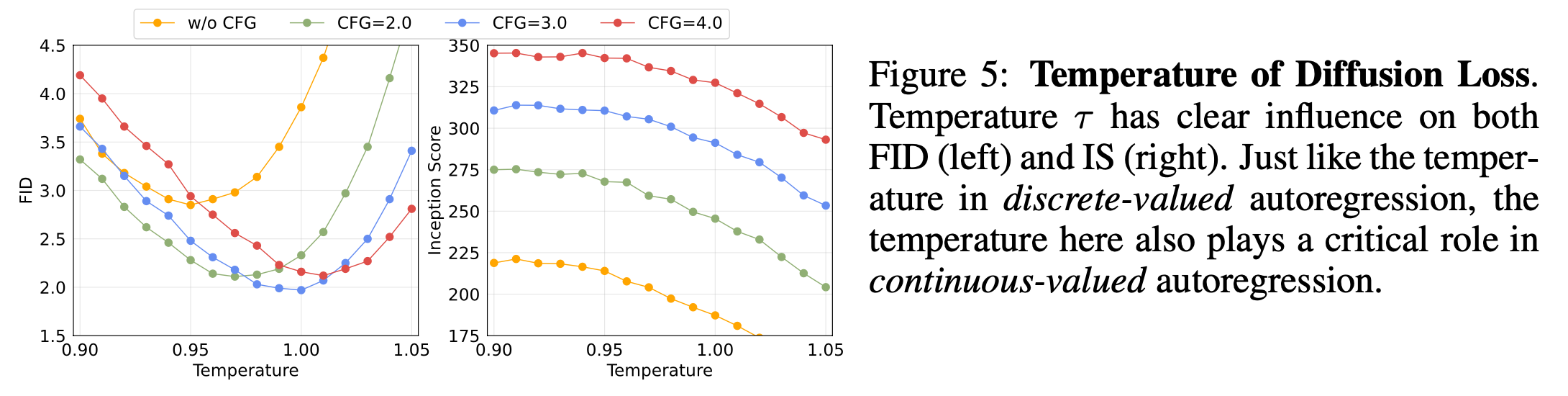
Temperature of Diffusion Loss
cross entropy loss와 마찬가지로, 추론 시 \(\tau\)가 중요하다고 합니다. \(\tau\)는 다양성과 정확성을 조절하며, 최적의 온도에서 최상의 성능을 달성.
5.2. Properties of Generalized Autoregressive Models
From AR to MAR
AR 모델에서 raster order에서 random order로 변경하면 FID가 19.23에서 13.07로 감소.
Causal Attention을 bidirectional Attention으로 변경하면 FID가 13.07에서 3.43으로 대폭 감소.
Predicting multiple tokens : 한 번에 여러 토큰을 예측하며 step수를 줄일 수 있지만, 살짝 성능이 떨어진다고 합니다.
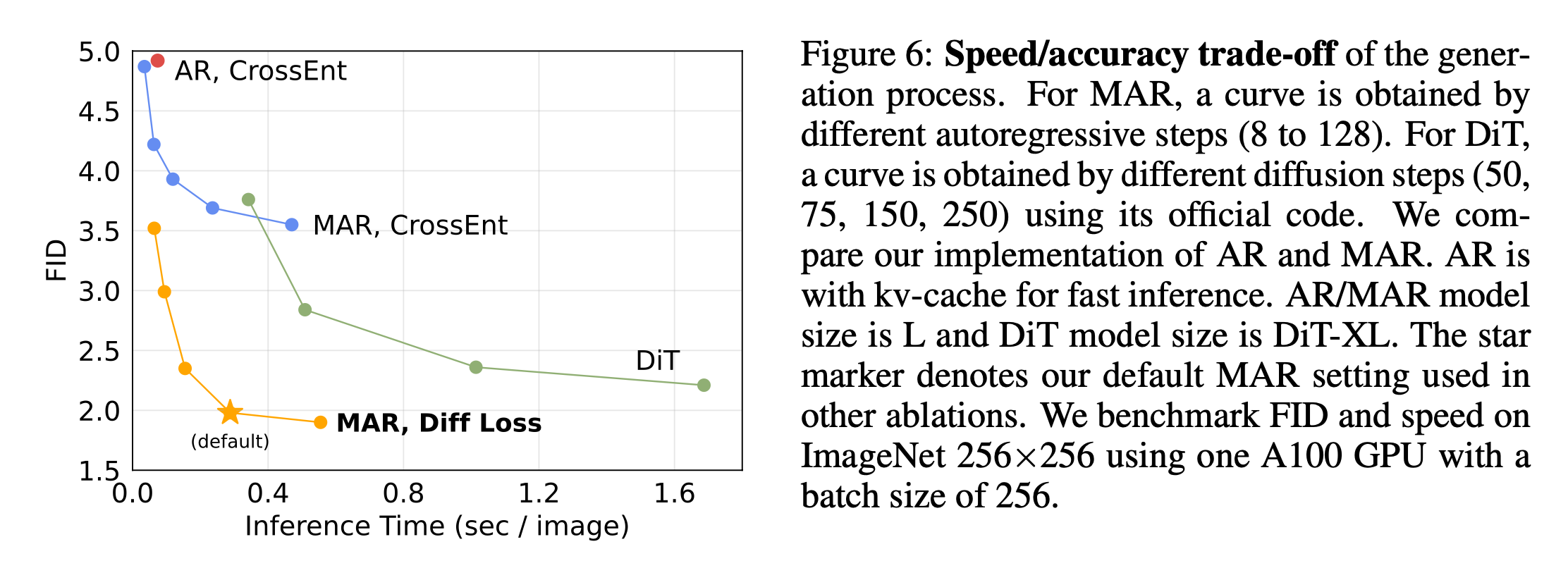
Speed/accuracy Trade-off
MaskGIT과 유사하게 MAR은 한 번에 여러 토큰을 예측할 수 있습니다. 저자들의 MAR은 여러개의 토큰을 동시에 예측하며 AR step수를 조절할 수 있다는 유연성을 가진다고 합니다.
또한 MAR은 최근 주목받는 Diffusion Transformer(DiT)와 비교해도 우수한 성능을 보인다고 합니다. DiT는 전체 Transformer 아키텍처를 사용하지만, MAR은 작은 MLP를 기반으로 작동합니다. 결과적으로, MAR은 더 빠르고 정확하며, FID < 2.0으로 < 0.3 second per image 생성 속도를 달성할 수 있었다고 합니다.