[Paper Reivew] Score-Based Generative Modeling through Stochastic Differential Equations (SDE)

ICLR 2021. [Paper] [Github]
Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, Ben Poole
Stanford University | Google Brain
26 Nov 2020

들어가며,,

수식 유도와 관련된 내용이 많아 읽기가 쉽지 않았네요…
틀린 내용이 있다면 언제든지 지적 부탁드립니다.

본격적으로 시작합니다!

TL;DR

논문의 저자들은 다음을 제시한다.

• 복잡한 데이터 분포에 점진적으로 노이즈를 더해가며, 알려진 prior 분포로 부드럽게 변환하는 SDE (data dist. + noise -> prior dist.)

• 위와 대응하는 점진적으로 노이즈를 제거하는과정인, reverse-time SDE (prior dist. - noise -> data dist.)

Score-based 생성 모델링으로, 저자들은 Neural Network를 이용해 이러한 score를 정확하게 예측할 수 있었으며, Numerical SDE solver을 이용해 이미지 샘플을 생성할 수 있었다고 한다.

이 Framework는 기존 score-based modeling, diffusion modeling을 포괄하며, 새로운 샘플링 절차와 모델링 능력을 제공한다.

1. INTRODUCTION

노이즈를 서서히 더해가며 training data를 noise로 바꾸고, 이러한 과정을 학습하여 거꾸로 noise를 제거하는 방식을 이용해 이미지를 생성할 수 있는 모델은 크게 2가지로 분류된다.

• Score matching with Langevin dynamics (SMLD)
• Denoising diffusion probabilistic modeling (DDPM)

하지만 이 두 방법 모두 기본적으로 score를 예측하는 모델이므로 흔히 score-based generative model이라하며, 이미지, 오디오, 그래프 등 여러 생성 분야에서 효과적임이 확인되어 왔다.

이에 저자들은 score-based generative model의 성능을 확장시키기 위해 이전 접근 방법들을 SDE를 이용해 일반화하여, 통합된 새로운 frame work를 제시한다.

특히, 유한한 noising step을 가하는 대신, 연속적인 diffusion process를 제시한다. 이 process는 서서히 data point를 nosie로 확산시키며, SDE는 data에 의존하지 않고 trainable parameter가 필요 없다고 한다.

이 과정을 거꾸로 뒤집어, random noise로부터 이미지를 생성할 수 있다고 한다. 이 과정은 forward SDE로부터 유도된 reverse-time SDE를 만족하는데, 저자들은 이 reverse-time SDE를 time-dependent Neural Net을 이용해 score를 효과적으로 예측하도록 모델링 했다. 이때 이미지 샘플은 Numerical SDE solver들을 이용한다.

Solving a reverse- time SDE yields a score-based generative model

저자들의 기여를 정리하자면 다음과 같다.

• Flexible sampling and likelihood computation : 샘플링을 위한 reverse-time SDE에서 어떤 SDE-solver든 사용할 수 있다고 한다.

  1. Predictor-Corrector(PC) Sampler : 기존 방법을 통합하고 개선
  2. Deterministic Sampler : black-box ODE solver를 통해, 빠른 적응형 샘플링, latent code를 이용한 유연한 데이터 조작, 고유하게 식별가능한 인코딩, 정확한 likelihood 계산.

• Controllable generation : 이후에 ADM(이전포스팅) Classifier Guidance로 적극적으로 활용함

• Unified framework : score-based 생성형 모델의 성능 향상을 위해, 통합된 framework를 제시.

2. BACKGROUND

SMLD와 DDPM의 간단한 설명입니다.

2.1. DENOISING SCORE MATCHING WITH LANGEVIN DYNAMICS (SMLD)

Score-based 생성 모델은 random noise에서부터, log-likelihood의 gradient(\(\nabla_x \log p(x)\))를 따라 이동하여, Langevin dynamics로 기존 데이터와 비슷한 이미지를 생성(샘플링)한다. 이때, \(\nabla_x \log p(x)\)를 추정하기 위해 \(s_\theta (x)\)를 학습하는 것이다.

\[\begin{equation} Loss = \frac{1}{2} \mathbb{E}_{p_{\textrm{data}}(x)} [ \| s_\theta (x) - \nabla_x \log p(x)\|_2^2 ] \end{equation}\]

Sampling

\[\begin{equation} x_{i+1} = x_i + \epsilon_i s_\theta (x_i) + \sqrt{2 \epsilon_i} z_i, \quad \quad z_i \sim \mathcal{N} (0, I) \end{equation}\]

위 방식을 개선한 방식이 Denoising Score Matching이라고 한다. 입력 데이터에 작은 Gasussian noise를 추가한 perturbed data dist. \(p_\sigma (\tilde{x} \vert x) := \mathcal{N}(\tilde{x}; x, \sigma^2 I)\)의 score도 원래 데이터의 score와 같다는 것을 이용한다.

\[\begin{aligned} Loss &= \frac{1}{2} \mathbb{E}_{p_{\textrm{data}}(x)} [ \| s_\theta (\tilde{x}, \sigma) - \nabla_x \log p_\sigma (\tilde{x} | x) \|_2^2 ] \\ &= \frac{1}{2} \mathbb{E}_{p_{\textrm{data}}(x)} [ \| s_\theta (\tilde{x}, \sigma) - \frac{\tilde{x} - x}{\sigma^2} \|_2^2 ] \end{aligned}\]

여기서 Song & Ermon (2019)이 Noise Conditional Score Network(NCNS, \(s_\theta (x, \sigma)\)) 를 denoising score matching objective들을 weighted sum하여 학습하는 방법을 제시하였다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \sum_{i=1}^N \sigma_i^2 \mathbb{E}_{p_{\textrm{data}}(x)} \mathbb{E}_{p_{\sigma_i}(\tilde{x}|x)} [\| s_\theta (\tilde{x}, \sigma_i) - \nabla_{\tilde{x}} \log p_{\sigma_i} (\tilde{x}|x) \|_2^2] \end{equation}\]

샘플링은 \(M\) step의 Langevin MCMC로 각 \(p_{\sigma_i} (x)\)를 샘플링한다.

\[\begin{equation} x_i^m = x_i^{m-1} + \epsilon_i s_{\theta^\ast} (x_i^{m-1}, \sigma_i) + \sqrt{2 \epsilon_i} z_i^m, \quad \quad m = 1, 2, \cdots, M \end{equation}\]

2.2. DENOISING DIFFUSION PROBABILISTIC MODELS (DDPM)

자세한 내용은 Diffusion Basic(이전 포스팅)를 참고하시면 좋습니다.

Forward Process :

미리 정해진 noise scheduling(\(0 < \beta_1, \beta_2, \cdots, \beta_N < 1\))에 따라, 특정 time step에서의 nosiy한 이미지는 다음과 같이 구할 수 있다.

\[\begin{equation} p_{\alpha_i} (x_i \vert x_0) = \mathcal{N} (x_i; \sqrt{\alpha_i} x_0, (1- \alpha_i)I), \quad \quad \alpha_i := \prod_{j=1}^i (1-\beta_j) \end{equation}\]

Reverse Process :

Noisy한 이미지로 부터 노이즈를 제거하는 reverse process는 다음과 같이 parameterization된다.

\[\begin{equation} p_\theta (x_{i-1} \vert x_i) = \mathcal{N}(x_{i-1}; \frac{1}{\sqrt{1-\beta_i}} (x_i + \beta_i s_\theta (x_i, i)), \beta_i I) \end{equation}\]

이때 \(s_{\theta} (x, i)\)의 trianing은 다음과 같은 ELBO를 이용한다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \sum_{i=1}^N (1-\alpha_i) \mathbb{E}_{p_\textrm{data} (x)} \mathbb{E}_{p_{\alpha_i} (\tilde{x} | x)} [\|s_\theta (\tilde{x}, i) - \nabla_{\tilde{x}} \log p_{\alpha_i} (\tilde{x} | x)\|_2^2] \end{equation}\]

학습이 완료되면 모델 \(s_{\theta^\ast} (x, i)\)로부터 이미지 생성(샘플링)이 가능하다.

\[\begin{equation} x_{i-1} = \frac{1}{\sqrt{1-\beta_i}} (x_i + \beta_i s_{\theta^\ast} (x_i, i)) + \sqrt{\beta_i} z_i, \quad \quad i = N, N-1, \cdots, 1 \end{equation}\]

3. SCORE-BASED GENERATIVE MODELING WITH SDES

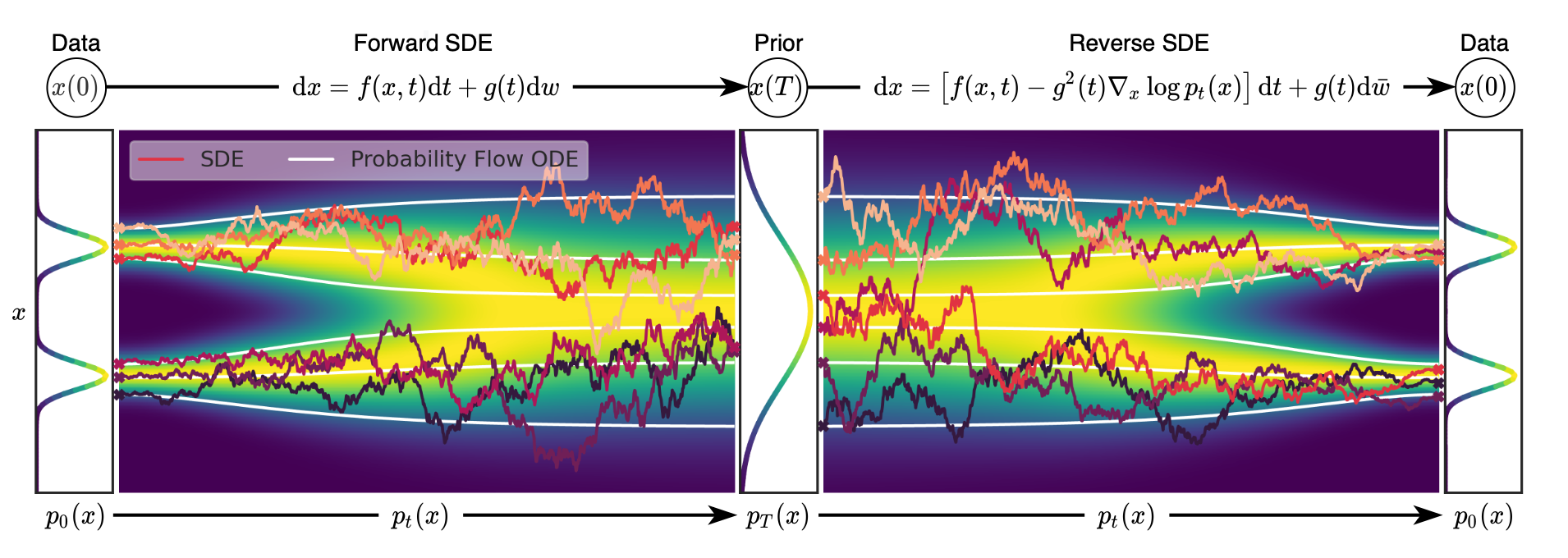Overview of score-based generative modeling through SDEs

3.1. PERTURBING DATA WITH SDES

저자들의 목표는 data dist. \(x(0) \sim p_0\), prior dist.\(x(T) \sim p_T\)가 되도록 diffusion process \(\{x(t)\}_{t=0}^T\)를 만드는 것이다. 이런 diffusion process는 다음과 같이 Itô SDE의 solution으로 모델링 할 수 있다.

\[\begin{equation} dx = f(x,t)dt + g(t)dw \end{equation}\]

여기서

• \(f(x,t)\)는 데이터의 결정적인 변화(드리프트) 항이며, 시간이 지남에 따라 데이터가 어떻게 이동하는지를 설명합니다.
• \(g(t)\)는 데이터에 주입되는 노이즈의 크기(확산 항)이다.
• \(dw\)는 Wiener process(브라운 운동)로, 시간에 따라 random한 노이즈가 데이터에 추가되는 것이다.

3.2. GENERATING SAMPLES BY REVERSING THE SDE

\(x(T) \sim p_T\) (\(p_0\)의 정보가 없는)로부터 reverse process를 통해 sampling이 시작된다. reverse-time SDE는 다음과 같다.

\[\begin{equation} dx = [f(x,t) - g(t)^2 \nabla_x \log p_t (x)] dt + g(t) d \bar{w} \end{equation}\]

여기서,

• \(\nabla_x \log{p_{t}(x)}\)는 스코어 함수로, 시간 \(t\)에서 데이터의 로그 확률 밀도의 기울기를 나타낸다.

• \(f(x,t)\)는 데이터의 결정적인 변화(드리프트)이며, Forward SDE와 동일하다.

• \(g(t)\)는 노이즈의 크기를 제어하며, Forward SDE와 동일하다.

• \(d\bar{w}\) 는 역방향으로 작용하는 무작위적인 노이즈이다.

만약 score function \(\nabla_x \log{p_{t}(x)}\)를 모든 \(t\)에 대해 알 수 있다면, 위 reverse diffusion process를 유도 할 수 있다. (따라서 위 score function을 제대로 추정하도록 neural net으로 학습하는 것이다)

3.3. ESTIMATING SCORES FOR THE SDE

그렇다면 score-based model을 어떻게 학습할 수 있을까?

\(\nabla_x \log{p_{t}(x)}\)를 추정하기 위해 time-dependent score-bsed model \(s_\theta (x, t)\)를 학습한다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \mathbb{E}_t \bigg\{ \lambda (t) \mathbb{E}_{x(0)} \mathbb{E}_{x(t)} [\| s_\theta (x(t), t) - \nabla_{x(t)} \log p_{0t} (x(t) | x(0) \|_2^2)] \bigg\} \end{equation}\]

참고! 일반적으로 위 식을 풀기 위해서는 transition kernel \(p_{0t} (x(t) \vert x(0))\)를 알아야한다. 일반적인 SDE에서 Kolmogorov’s forward equation을 풀어 \(p_{0t} (x(t) \vert x(0))\)을 구할 수 있다. 하지만 저자들은 \(p_{0t} (x(t) \vert x(0))\)로부터 샘플링하기 위해 SDE를 시뮬레이션한뒤, denoising score matching을 sliced score matching으로 대체하는 방법을 사용했다고 한다. 그렇게 함으로써 \(\nabla_{x(t)} \log p_{0t} (x(t) | x(0))\) 계산을 안해도 된다고 한다

3.4. EXAMPLES: VE, VP SDES AND BEYOND

(수식은 너무 복잡해서 결론만 정리했습니다. Appendix B 참고)

결론적으로 SMLD와 DDPM의 noise perturbation은 SDE의 discretization에 대응된다는 것이다.

• SMLD의 SDE는 Variance Exploding(VE) SDE

• DDPM의 SDE는 Variance Preserving(VP) SDE라 한다.

저자들은 VP SDE에서 영감을 받아, likelihood에서 특히 잘 동작하는 새로운 타입의 SDE(sub-VP SDE)를 제안한다.

\[\begin{equation} dx = -\frac{1}{2} \beta(t) x dt + \sqrt{\beta (t) (1-e^{-2 \int_0^t \beta(s) ds})} dw \end{equation}\]

VE, VP, sub-VP SDE는 모두 affine drift coefficient를 갖기 때문에 각 perturbation kernel \(p_{0t} (x(t) \vert x(0))\)은 Gaussian이며, 모두 closed-form으로 계산 가능하다고 한다. (럭키비키~)

4. SOLVING THE REVERSE SDE

score-based model \(s_\theta\)를 학습한 이후, 이를 이용해 reverse-time SDE를 구성할 수 있으며, numerical approach를 통해 \(p_0\)로부터 이미지를 생성(샘플링)할 수 있다.

4.1. GENERAL-PURPOSE NUMERICAL SDE SOLVERS

Euler-Maruyama, stochastic Runge-Kutta methods와 같은 general-purpose SDE solver가 있다. 하지만 DDPM과 같이 reverse-time VP SDE에서 적용되는 solver를 유도하는 것은 non-trivial하다는 문제가 있다.

이에 저자들은 _reverse diffusion sampler_를 제안한다. Forward SDE와 동일한 방식으로 reverse-time SDE를 discretize하는 방법으로 forward discretization으로부터 쉽게 유도된다.

4.2. PREDICTOR-CORRECTOR SAMPLERS

일반적인 SDE와는 다르게, score-based model \(s_{\theta^\ast}(x, t) \approx \nabla_x \log{p_t(x)}\)의 추가적인 정보를 알고 있으므로, 이를 이용해 향상된 solution을 얻을 수 있다. score-based MCMC 접근법을 사용하여, \(p_t\)로부터 직접 샘플링하고, numerical SDE solver의 solution을 correction 하는 방법이다.

Predictor : “각 time step에서 numerical SDE solver는 먼저 sample에 대한 추정치를 준다.
Corrector : score-based MCMC 접근법을 활용하여, marginal dist를 correction한다.

(당연하게도) 실험 결과 Predictor만 쓰는 경우, Corrector만 쓰는 경우와 비교해, PC 방식을 이용하는 것이 항상 가장 좋은 성능을 냈다고 한다.

Comparing different reverse-time SDE solvers on CIFAR-10

4.3. PROBABILITY FLOW AND CONNECTION TO NEURAL ODES

deterministic process 의 경우 marginal probability density \(\{p_t (x)\}_{t=0}^T\)르라 공유하기 한다. 이 process는 다음 ODE를 만족한다.

\[\begin{equation} dx = \bigg[ f(x,t) - \frac{1}{2} g(t)^2 \nabla_x \log p_t (x) \bigg] dt \end{equation}\]

이를 저자들은 probability flow ODE 라 부르기로 했다. 또한 이때 score function은 time-dependent score-based model로 추정(Neural Net으로 학습)되므로, neural ODE의 예시이기도 하다.

다음의 의의를 갖는다.

1. Exact likelihood computation

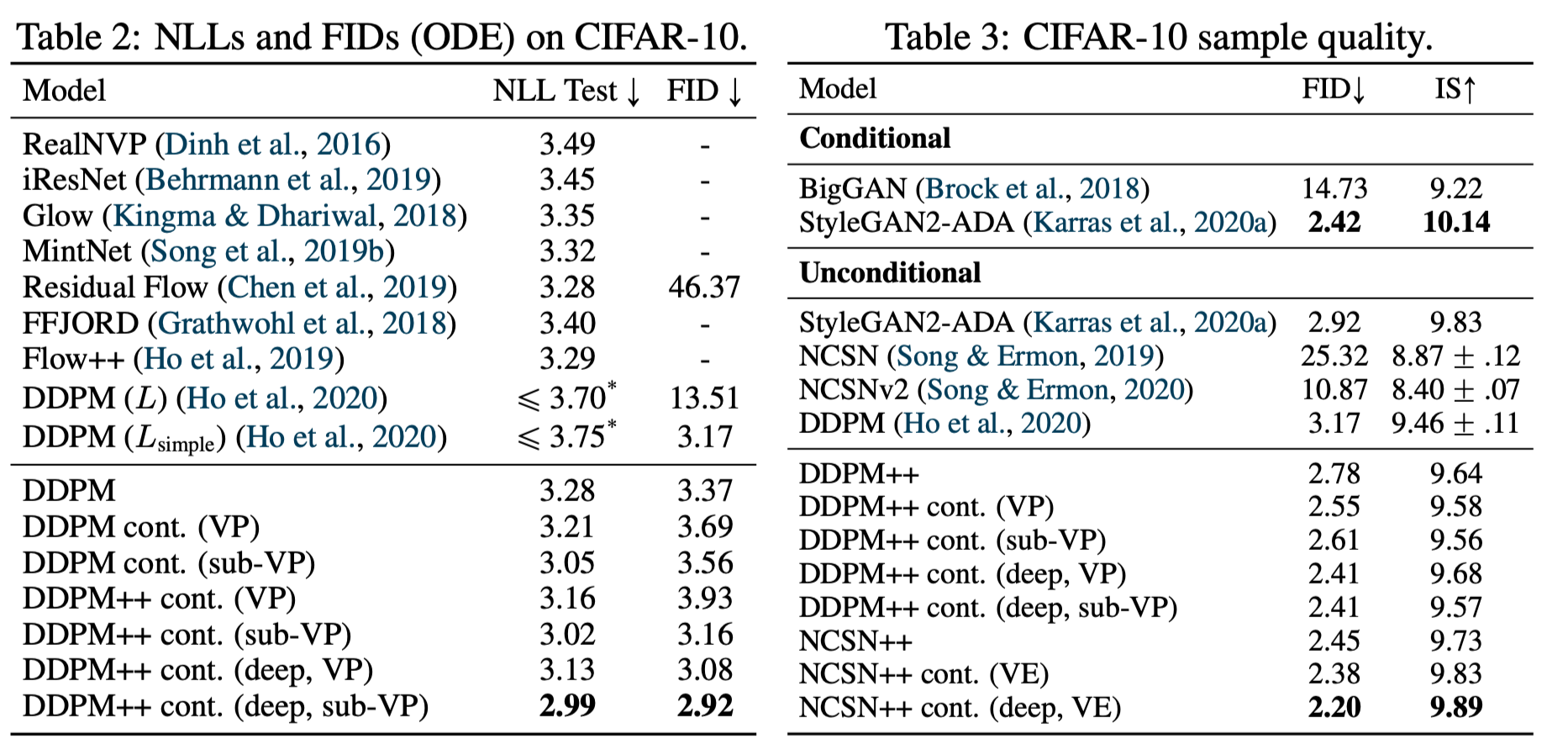
임의의 input data에서도 exact likelihood를 계산할 수 있다. 주요한 실험결과는 다음과 같다.

1. 같은 DDPM model을 사용한 경우 저자들의 bits/dim이 ELBO에 비해 더 좋았다.
2. 같은 arichtecture를 사용한 경우, continuous objective로 학습한 모델의 likelihood가 향상되었다.
3. sub-VP를 사용하는 경우, VP를 사용할 때보다 항상 높은 likelihood를 얻었다.
4. 향상된 architecture(DDPM++ cont.)와 sub-VP를 함께 사용하는 경우, SOTA 성능을 기록하였다.

2. Manipulating latent representations

\(x(0)\)에서 latent space \(x(T)\)로부터 encoding이 가능하고, 대응하는 ODE를 이용해 decoding도 가능하다. 이로인해 저자들은 latent space representation을 조작할 수 있다고 한다. 이런 특성은 interpolation이나 temperature scaling 같은 image editing을 가능하게 한다.

3. Uniquely identifiable encoding

최근 대부분의 invertible model들과는 다르게, 저자들의 (충분한 capa를 갖고 적절히 학습된 모델의) encoding은 uniquely identifiable 하다고 한다. 이는 저자들의 forward SDE가 학습 가능한 parameter가 없기 때문이다.

4. Efficient sampling

저자들은 Black-box ODE solver를 사용하면서, 높은 품질의 이미지를 생성뿐만 아니라, accuracy와 efficient사이 trade-offf를 가능하도록 한다고 한다.

4.4. ARCHITECTURE IMPROVEMENTS

저자들은 또한 새로운 model architecture를 실험하였다. 개선된 세부사항은 다음과 같다.

1. Finite Impulse Response를 기반으로 한 anti-aliasing으로 upsampling과 downsampling 진행
2. 모든 skip connection을 \({\frac{1}{\sqrt{2}}\)로 rescaling (GAN에서 주로 사용하는 방법)
3. 기존 residual block을 BigGAN의 residual block으로 대체
4. 각 resolution에 대한 residual block의 개수를 2에서 4로 늘림
5. Incorporating progressive growing architectures (StyleGAN-2에서 사용)

5. CONTROLLABLE GENERATION

Conditional Score function \(\nabla _x \log{p_t(x \vert y)}\)에서 Bayes’ Rule을 이용하여, 다음과 같이 표현할 수 있다.

\[\begin{equation} \log{p(x \vert y)} = \log{p(y \vert x)} + \log{p(x)} - \log{p(y)} \end{equation}\]

이를 \(x\)에 대해 미분을 취하면 다음과 같다.

\[\begin{equation} \nabla_x \log{p(x \vert y)} = \nabla_x \log{p(y \vert x)} + \nabla_x \log{p(x)} \end{equation}\]

이를 reverse-time SDE에 적용하면 다음과 같다.

\[\begin{equation} dx = \{ f(x,t) - g(t)^2 [\nabla_x \log p_t (x) + \nabla_x \log p_t (y | x)] \} dt + g(t) d \bar{w} \end{equation}\]

\(\nabla_x \log p_t (x)\)는 unconditional score function이며, \(\nabla_x \log p_t (y | x)\)는 classifier를 의미한다. 즉 pretrained unconditional diffusion model에 classifier를 이용하면 conditional 이미지 생성이 가능하다는 것이다.

ADM(이전 포스팅)에서 위 논문의 결과를 활용해 Diffusion model로 GAN의 성능을 능가했습니다.

6. CONCLUSION

저자들은 SDE를 기반으로 한 score-based 생성 모델링 framework를 제시하여 기존 접근법에 대한 이해를 높이고, 새로운 sampling algorithm과 exact likelihood 계산, uniquely encoding, latent code manipulation 및 conditional generation 능력을 제공한다.

Reference

JiYeop Kim’s blog를 참고하여 작성하였습니다.