[Paper Reivew] Neural Discrete Representation Learning & Generating Diverse High-Fidelity Images with VQ-VAE-2

Neural Discrete Representation Learning
NeurIPS 2017 [Paper]
Aaron van den Oord, Oriol Vinyals, Koray Kavukcuoglu
DeepMind
30 May 2018

TL;DR

VAE framework를 discrete latent space에서 사용하는 VQ-VAE 방법론을 제안

1. Introduction

저자들의 목표는 Latent space에서 중요한 feature를 보존하는 model을 구성하는 것이라고 합니다. 저자들은 VAE framework를 discrete latent space에서 사용하는 VQ-VAE 방법론을 제안합니다. 학습이 쉬우며 기존 VAE에서 발생하는 posterior collapse 문제가 없다는 장점이 있다고 합니다.

• Discrete latent model로 continuous model과 비슷한 성능
• Powerful prior 이용해 높은 생성 퀄리티

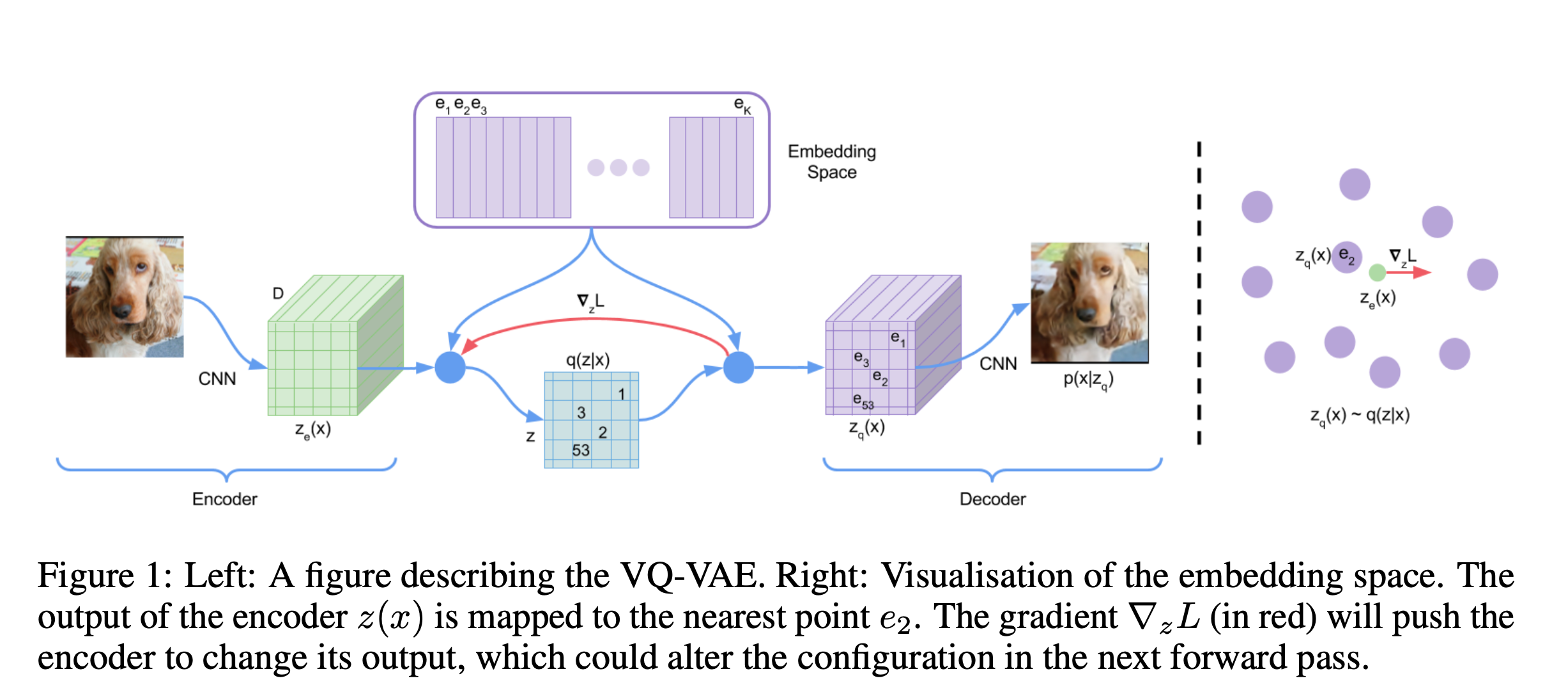
2. VQ-VAE

2.1. Discrete Latent variables

Latent embedding space \(e \in \mathbb{R}^{K \times D}\)를 정의하는데, 이때 \(K\)는 discrete latent space의 크기( \(K\)-way categorical, 각 embedding vector는 \(D\)-dim). Encoder 통과시킨 뒤 codebook에서 nearest neighbour look-up 과정을 통해 codebook의 index만 저장.

\[q(z = k \mid x) = \begin{cases} 1 & \text{for } k = \arg\min_{j} \| z_e(x) - e_j \|_2, \\ 0 & \text{otherwise.} \end{cases}\]

따라서 quantized 된 인코더의 출력은 다음과 같습니다.

\[z_q(x) = e_k, \quad \text{where } k = \arg\min_{j} \| z_e(x) - e_j \|_2.\]

여기서 생각해볼 것은, 위 식의 real gradient는 정의되지 않는다는 것입니다. 따라서 저자들은 decoder의 gradient를 encoder에 그대로 흘려주는 방식으로 이를 approximate 했다고 합니다.

2.2. Learning

learning objective는 3가지로 구성됩니다.

\[\mathcal{L}(\mathbf{x}, D(\mathbf{e})) = \| \mathbf{x} - D(\mathbf{e}) \|_2^2 + \| \text{sg}[E(\mathbf{x})] - \mathbf{e} \|_2^2 + \beta \| \text{sg}[\mathbf{e}] - E(\mathbf{x}) \|_2^2\]

1. Reconstruction loss : encode/decode 과정을 거친 이미지와 원본 이미지 비교.
2. Codebook loss : 인코더는 freeze하고 codebook만 업데이트.
3. Commitment loss : codebook은 freeze하고 encoder만 업데이트.

---

Generating Diverse High-Fidelity Images with VQ-VAE-2
NeurIPS 2019 [Paper]
Ali Razavi, Aaron van den Oord, Oriol Vinyals
DeepMind
2 Jun 2019

TL;DR

VQ-VAE에서 hierarchical 구조, Latent code의 prior학습을 통해 VQ-VAE2 제안.

1. Introduction

VQ-VAE를 업그레이드 한 방식인 VQ-VAE2를 제안합니다. Lossy compression의 아이디어를 활용해서 생성모델이 사소한 정보를 모델링 하지 않도록 하면서, VQ-VAE와 같이 VQ-quantization을 활용해 discrete latent space로 이미지를 압축하는 것입니다. 메인 아이디어는 크게 2가지 입니다.

1. Learning Hierarchical Latent Codes
2. Learning Priors over Latent Codes

2. Method

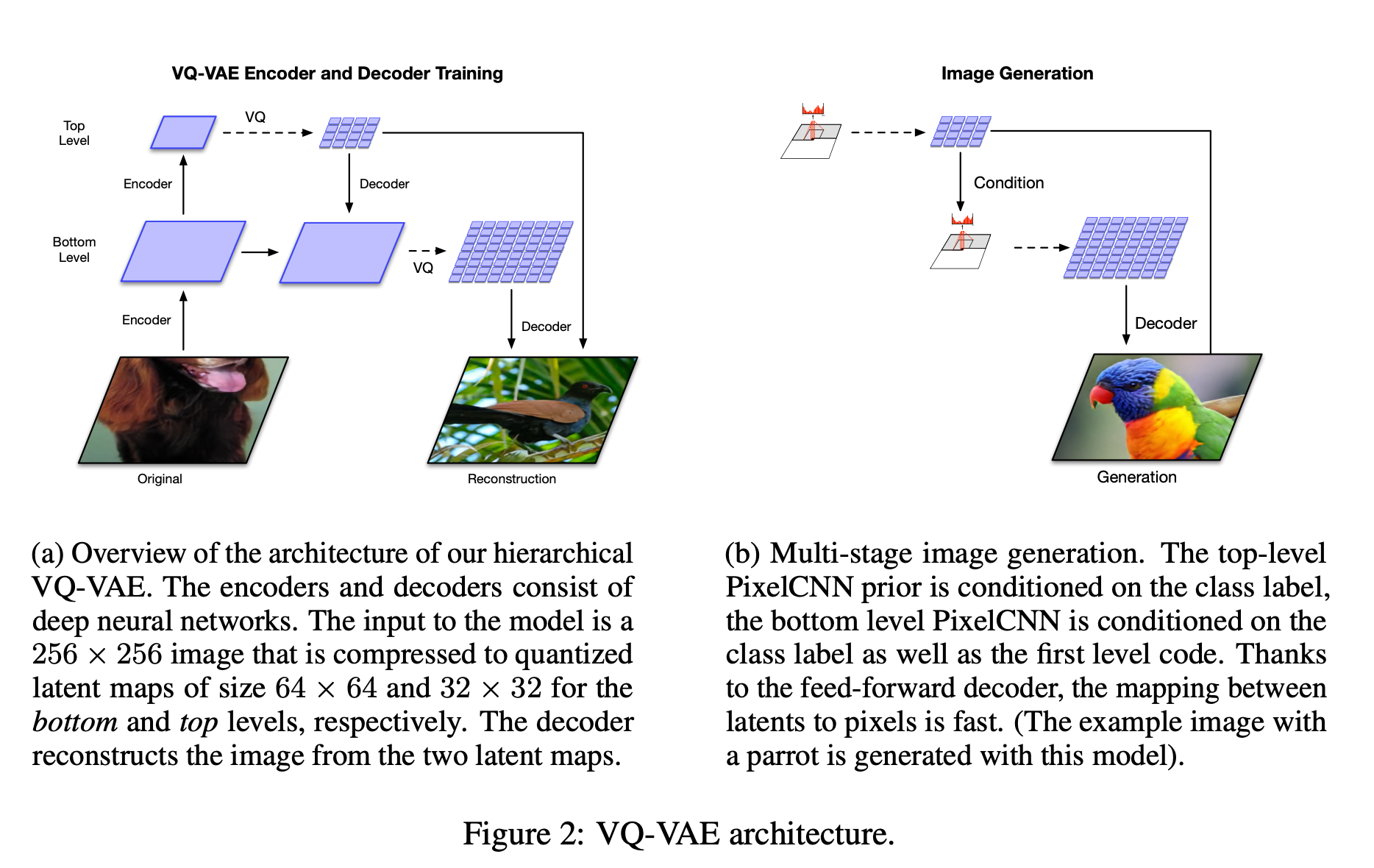
2.1. Learning Hierarchical Latent Codes

VQ-VAE와는 다르게 hierarchical 구조를 사용합니다. Global, local 정보를 나눠서 학습하기 위함이라고 합니다.

1. Global : Shape, Geometry 같은 정보, Top level에서 학습.
2. Lcoal : Texture 같은 정보, Bottom level에서 학습.

3.2. Learning Priors over Latent Codes

학습 데이터로부터 prior distribution을 fitting하는 것은 성능을 크게 향상 시킬 수 있다고 합니다. Information theory 관점에서는 이 과정을 lossless compression으로 볼 수 있으며, latent variable을 re-encoding하여 더 정확한 분포로 근사하는 것이라고 합니다.

VQ-VAE2에서는 PixelCNN과 같은 강력한 AR모델을 사용해 auxiliary prior를 모델링 했다고 합니다.